
【題目】設f(x)=x2lnx,g(x)=ax3﹣x2 .
(1)求函數f(x)的最小值;
(2)若存在x∈(0,+∞),使f(x)>g(x),求實數a的取值范圍;
(3)若使方程f(x)﹣g(x)=0在x∈[ ![]() ,en](其中e=2.7…為自然對數的底數)上有解的最小a的值為an , 數列{an}的前n項和為Sn , 求證:Sn<3.
,en](其中e=2.7…為自然對數的底數)上有解的最小a的值為an , 數列{an}的前n項和為Sn , 求證:Sn<3.
【答案】
(1)解:f(x)=x2lnx的導數為f′(x)=2xlnx+x=x(1+2lnx),x>0,
當x> ![]() 時,f′(x)>0,f(x)遞增;當0<x<
時,f′(x)>0,f(x)遞增;當0<x< ![]() 時,f′(x)<0,f(x)遞減.
時,f′(x)<0,f(x)遞減.
即有x= ![]() 處取得極小值,也為最小值﹣
處取得極小值,也為最小值﹣ ![]()
(2)解:存在x∈(0,+∞),使f(x)>g(x),
即為a< ![]() 在(0,+∞)成立,
在(0,+∞)成立,
設h(x)= ![]() ,h′(x)=
,h′(x)= ![]() =﹣
=﹣ ![]() ,
,
當x>1時,h′(x)<0,h(x)遞減;當0<x<1時,h′(x)>0,h(x)遞增.
即有x=1處取得極大值,也為最大值1,
則a<1,即a的取值范圍是(﹣∞,1)
(3)證明:方程f(x)﹣g(x)=0,即為a= ![]() 在x∈[
在x∈[ ![]() ,en]上有解,
,en]上有解,
由(2)可得h(x)= ![]() 在(
在( ![]() ,1)遞增,在(1,en]遞減,
,1)遞增,在(1,en]遞減,
由 ![]() <en,可得x=en處取得最小值,且為(1+n)e﹣n,
<en,可得x=en處取得最小值,且為(1+n)e﹣n,
前n項和為Sn=2e﹣1+3e﹣2+4e﹣3+…+(1+n)e﹣n,
eSn=2e0+3e﹣1+4e﹣2+…+(1+n)e1﹣n,
相減可得,(e﹣1)Sn=2+e﹣1+e﹣2+e﹣3+…+e1﹣n﹣(1+n)e﹣n
=1+ ![]() ﹣﹣(1+n)e﹣n
﹣﹣(1+n)e﹣n
化簡可得Sn= ![]() ﹣
﹣ ![]() e﹣n(
e﹣n( ![]() +n+1)<
+n+1)< ![]() <3.
<3.
故Sn<3成立
【解析】(1)求出函數f(x)的導數,求得單調區間和極值,即可得到最小值;(2)由題意可得a< ![]() 在(0,+∞)成立,設h(x)=
在(0,+∞)成立,設h(x)= ![]() ,求出導數,求得單調區間和極值,最大值,即可得到a的范圍;(3)方程f(x)﹣g(x)=0,即為a=
,求出導數,求得單調區間和極值,最大值,即可得到a的范圍;(3)方程f(x)﹣g(x)=0,即為a= ![]() 在x∈[
在x∈[ ![]() ,en]上有解,求得h(x)在x∈[
,en]上有解,求得h(x)在x∈[ ![]() ,en]上的最小值,可得an=(1+n)e﹣n , 由錯位相減法求得Sn , 再由不等式的性質即可得證.
,en]上的最小值,可得an=(1+n)e﹣n , 由錯位相減法求得Sn , 再由不等式的性質即可得證.
【考點精析】認真審題,首先需要了解利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減),還要掌握函數的最大(小)值與導數(求函數
在這個區間單調遞減),還要掌握函數的最大(小)值與導數(求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值)的相關知識才是答題的關鍵.
比較,其中最大的是一個最大值,最小的是最小值)的相關知識才是答題的關鍵.


 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:高中數學 來源: 題型:
【題目】動圓M與定圓C:x2+y2+4x=0相外切,且與直線l:x-2=0相切,則動圓M的圓心的軌跡方程為( )
A. y2-12x+12=0 B. y2+12x-12=0
C. y2+8x=0 D. y2-8x=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義域為R的偶函數. 當x≥0時,f(x)= 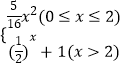 ,若關于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且僅有6個不同實數根,則實數a的取值范圍是 .
,若關于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且僅有6個不同實數根,則實數a的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某創業投資公司擬投資開發某種新能源產品,估計能獲得10萬元到1000萬元的投資收益.現準備制定一個對科研課題組的獎勵方案:獎金y(單位:萬元)隨投資收益x(單位:萬元)的增加而增加,且獎金不超過9萬元,同時獎金不超過投資收益的20%.
(1)若建立函數y=f(x)模型制定獎勵方案,試用數學語言表述該公司對獎勵函數f(x)模型的基本要求,并分析函數y= ![]() 是否符合公司要求的獎勵函數模型,并說明原因;
是否符合公司要求的獎勵函數模型,并說明原因;
(2)若該公司采用模型函數y= ![]() 作為獎勵函數模型,試確定最小的正整數a的值.
作為獎勵函數模型,試確定最小的正整數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A={x|x2-ax+a2-19=0},B={ x|x2-5x+6=0},C={x|x2+2x-8=0},且![]()
![]() (A∩B),A∩C=
(A∩B),A∩C=![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點與拋物線
的右焦點與拋物線![]() 的焦點重合,且該橢圓的離心率與雙曲線
的焦點重合,且該橢圓的離心率與雙曲線![]() 的離心率互為倒數.
的離心率互為倒數.
(1)求橢圓的方程;
(2)設直線![]() 與橢圓相交于不同的兩點
與橢圓相交于不同的兩點![]() ,已知點
,已知點![]() 的坐標為
的坐標為![]() ,點
,點![]() 在線段
在線段![]() 的垂直平分線上,且
的垂直平分線上,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com