已知二次函數f(x)=ax2+bx (a,b為常數,且a≠0),滿足條件f(1+x)=f(1-x),且方程f(x)=x有等根.
(1)求f(x)的解析式;
(2)是否存在實數m、n(m<n),使f(x)的定義域和值域分別為[m,n]和[3m,3n],如果存在,求出m、n的值,如果不存在,說明理由.
【答案】
分析:(1)由已知中f (1+x)=f (1-x),可得f(x)的圖象關于直線x=1對稱,結合方程f (x)=x有等根其△=0,我們可構造關于a,b的方程組,解方程組求出a,b的值,即可得到f (x)的解析式;
(2)由(1)中函數的解析式,我們根據f(x)的定義域和值域分別為[m,n]和[3m,3n],我們易判斷出函數在[m,n]的單調性,進而構造出滿足條件的方程,解方程即可得到答案.
解答:解:(1)∵f(x)滿足f(1+x)=f(1-x),∴f(x)的圖象關于直線x=1對稱.
而二次函數f(x)的對稱軸為x=-
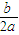
,∴-
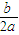
=1.①
又f(x)=x有等根,即ax
2+(b-1)x=0有等根,∴△=(b-1)
2=0.②
由①,②得 b=1,a=-

.∴f(x)=-

x
2+x.
(2)∵f(x)=-

x
2+x=-

(x-1)
2+

≤

.
如果存在滿足要求的m,n,則必需3n≤

,∴n≤

.
從而m<n≤

<1,而x≤1,f(x)單調遞增,
∴
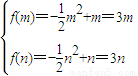
,
可解得m=-4,n=0滿足要求.
∴存在m=-4,n=0滿足要求.
點評:本題考查的知識點是二次函數的性質,其中(1)的關鍵是由已知條件構造關于a,b的方程組,(2)的關鍵是根據函數的值域判斷出函數在[m,n]的單調性,進而構造出滿足條件的方程.

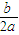 ,∴-
,∴-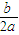 =1.①
=1.① .∴f(x)=-
.∴f(x)=- x2+x.
x2+x. x2+x=-
x2+x=- (x-1)2+
(x-1)2+ ≤
≤ .
. ,∴n≤
,∴n≤ .
. <1,而x≤1,f(x)單調遞增,
<1,而x≤1,f(x)單調遞增,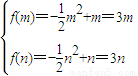 ,
,
