
【題目】2015男籃亞錦賽決賽階段,中國男籃以9連勝的不敗戰績贏得28屆亞錦賽冠軍,同時拿到亞洲唯一1張直通里約奧運會的入場券.賽后,中國男籃主力易建聯榮膺本屆亞錦賽![]() (最有價值球員),下表是易建聯在這9場比賽中投籃的統計數據.
(最有價值球員),下表是易建聯在這9場比賽中投籃的統計數據.
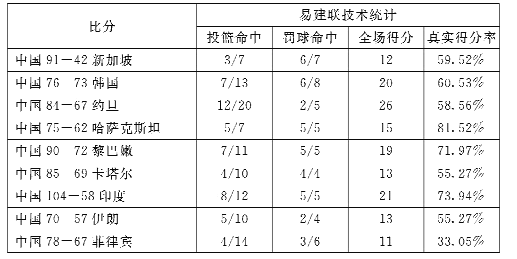
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真實得分率)是衡量球員進攻的效率,其計算公式為:
(真實得分率)是衡量球員進攻的效率,其計算公式為:
![]()
(1)從上述9場比賽中隨機選擇一場,求易建聯在該場比賽中![]() 超過
超過![]() 的概率;
的概率;
(2)我們把比分分差不超過15分的比賽稱為“膠著比賽”.為了考察易建聯在“膠著比賽”中的發揮情況,從“膠著比賽”中隨機選擇兩場,求易建聯在這兩場比賽中![]() 至少有一場超過
至少有一場超過![]() 的概率;
的概率;
(3)用![]() 來表示易建聯某場的得分,用
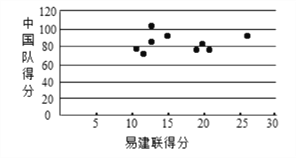
來表示易建聯某場的得分,用![]() 來表示中國隊該場的總分,畫出散點圖如圖所示,請根據散點圖判斷
來表示中國隊該場的總分,畫出散點圖如圖所示,請根據散點圖判斷![]() 與
與![]() 之間是否具有線性相關關系?結合實際簡單說明理由.
之間是否具有線性相關關系?結合實際簡單說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不具有線性相關關系.
;(3)不具有線性相關關系.
【解析】試題分析:(1)由已知,結合古典概型計算公式可得:易建聯在該場比賽中![]() 超過
超過![]() 的概率;(2)由已知,結合古典概型計算公式可得: 易建聯在該場比賽中
的概率;(2)由已知,結合古典概型計算公式可得: 易建聯在該場比賽中![]() 超過
超過![]() 的概率;(3)根據散點圖,并不是分布在某一條直線的周圍,可得結論.
的概率;(3)根據散點圖,并不是分布在某一條直線的周圍,可得結論.
試題解析:(1)設易建聯在比賽中![]() 超過
超過![]() 為事件
為事件![]() ,則共有8場比賽中
,則共有8場比賽中![]() 超過
超過![]() ,故
,故![]() ,
,
(2)設“易建聯在這兩場比賽中![]() 至少有一場超過
至少有一場超過![]() ”為事件
”為事件![]() ,則從上述9場比賽中隨機選擇兩場共有
,則從上述9場比賽中隨機選擇兩場共有![]() 個基本事件,而從中任意選擇兩場中,兩場
個基本事件,而從中任意選擇兩場中,兩場![]() 都不超過
都不超過![]() 的有
的有![]() 個基本事件,那么兩場至少有一場超過
個基本事件,那么兩場至少有一場超過![]() 的基本事件為
的基本事件為![]() 個基本事件.
個基本事件.
![]() .
.
(3)不具有線性相關關系.因為散點圖并不是分布在某一條直線的周圍.籃球是集體運動,個人無法完全主宰一場比賽.


科目:高中數學 來源: 題型:
【題目】選修4![]() 4:坐標系與參數方程
4:坐標系與參數方程
在直角坐標系![]() 中,已知直線l1:
中,已知直線l1: ![]() (
(![]() ,
, ![]() ),拋物線C:
),拋物線C:  (t為參數).以原點
(t為參數).以原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求直線l1 和拋物線C的極坐標方程;
(Ⅱ)若直線l1 和拋物線C相交于點A(異于原點O),過原點作與l1垂直的直線l2,l2和拋物線C相交于點B(異于原點O),求△OAB的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知平面直角坐標系![]() ,以
,以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系,
軸的非負半軸為極軸建立極坐標系, ![]() 點的極坐標為
點的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)寫出點![]() 的直角坐標及曲線
的直角坐標及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的中點
的中點![]() 到直線
到直線![]() :
: ![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各組函數f(x)與g(x)的圖象相同的是( )
A.f(x)=x,g(x)=( ![]() )2
)2
B.f(x)=x2 , g(x)=(x+1)2
C.f(x)=1,g(x)=x0
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解消費者購物情況,某購物中心在電腦小票中隨機抽取![]() 張進行統計,將結果分成6組,分別是:
張進行統計,將結果分成6組,分別是: ![]() ,
, ![]() ,制成如下所示的頻率分布直方圖(假設消費金額均在
,制成如下所示的頻率分布直方圖(假設消費金額均在![]() 元的區間內).
元的區間內).
(1)若在消費金額為![]() 元區間內按分層抽樣抽取6張電腦小票,再從中任選2張,求這2張小票來自
元區間內按分層抽樣抽取6張電腦小票,再從中任選2張,求這2張小票來自![]() 元和
元和![]() 元區間(兩區間都有)的概率;
元區間(兩區間都有)的概率;
(2)為做好春節期間的商場促銷活動,商場設計了兩種不同的促銷方案.

方案一:全場商品打八五折.
方案二:全場購物滿100元減20元,滿300元減80元,滿500元減120元,以上減免只取最高優惠,不重復減免.利用直方圖的信息分析:哪種方案優惠力度更大,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com