
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)令![]() ,設數列
,設數列![]() 的前
的前![]() 項和為
項和為![]() ,求
,求![]() ;
;
(3)令![]() ,若
,若![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ; (2)
; (2) ![]() ;(3)
;(3) ![]()
【解析】試題分析:(1) 當![]() 時,利用公式
時,利用公式![]() ;,可得
;,可得![]() ,驗證當
,驗證當![]() 時是否適合即可;(2)由(1)可得
時是否適合即可;(2)由(1)可得![]() ,利用錯位相減法求和即可(3)討論當
,利用錯位相減法求和即可(3)討論當![]() 為奇數時,當
為奇數時,當![]() 為偶數時兩種情況,分別利用等差數列求和公式求和,然后利用放縮法可證明結論.
為偶數時兩種情況,分別利用等差數列求和公式求和,然后利用放縮法可證明結論.
試題解析:(I)當![]() 時,
時, ![]()
當![]() 時,
時, ![]() ,適合上式,
,適合上式,
![]()
![]() (
(![]() ).
).
(II) ![]() ,則
,則![]() ,
,
![]() ,
,
-得
![]() ,
,
![]() .
.
![]() .
.
(III) ![]() ,
,
當![]() 為奇數時,
為奇數時, ![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
當![]() 為偶數時,
為偶數時, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
綜上所述, ![]()
【 方法點睛】本題主要考查等差數列的通項與求和公式以及錯位相減法求數列的的前![]() 項和,屬于中檔題.一般地,如果數列
項和,屬于中檔題.一般地,如果數列![]() 是等差數列,
是等差數列, ![]() 是等比數列,求數列
是等比數列,求數列![]() 的前
的前![]() 項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列
項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列![]() 的公比,然后作差求解, 在寫出“
的公比,然后作差求解, 在寫出“![]() ”與“
”與“![]() ” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“
” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“![]() ”的表達式.
”的表達式.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】某中學將100名高二文科生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班進行教改實驗.為了了解教學效果,期末考試后,陳老師對甲、乙兩個班級的學生成績進行統計分析,畫出頻率分布直方圖(如下圖).記成績不低于90分者為“成績優秀”.
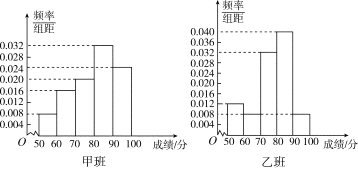
(Ⅰ)根據頻率分布直方圖填寫下面2×2列聯表;
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
(Ⅱ)判斷能否在犯錯誤的概率不超過0.05的前提下認為:“成績優秀”與教學方式有關?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列四個命題:
①“若![]() , 則
, 則![]() 互為相反數”的逆命題;
互為相反數”的逆命題;
②“若兩個三角形全等,則兩個三角形的面積相等”的否命題;
③“若![]() ,則
,則![]() 有實根”的逆否命題;
有實根”的逆否命題;
④“若![]() 不是等邊三角形,則
不是等邊三角形,則![]() 的三個內角相等”逆命題;
的三個內角相等”逆命題;
其中真命題為( ).
A. ①② B. ②③ C. ①③ D. ③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點的動直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,
, ![]() .
.
(1)求圓![]() 的圓心坐標;
的圓心坐標;
(2)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)是否存在實數![]() ,使得直線
,使得直線![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直四棱柱ABCD﹣A1B1C1D1中,DB=BC,DB⊥AC,點M是棱BB1上一點.
(1)求證:B1D1∥面A1BD;
(2)求證:MD⊥AC;
(3)試確定點M的位置,使得平面DMC1⊥平面CC1D1D.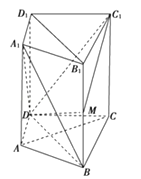
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com