【題目】設
、
是兩條不同的直線，
、
是兩個不同的平面，則下列四個命題：
①若
，
，則∥②若∥，
，則
③若，，則∥④若，，
，則
其中正確的命題序號是________
科目：高中數學 來源： 題型：
【題目】某行業主管部門為了解本行業中小企業的生產情況，隨機調查了100個企業，得到這些企業第一季度相對于前一年第一季度產值增長率y的頻數分布表.
|
|
|
|
|
|
企業數 | 2 | 24 | 53 | 14 | 7 |
（1）分別估計這類企業中產值增長率不低于40%的企業比例、產值負增長的企業比例；
（2）求這類企業產值增長率的平均數與標準差的估計值（同一組中的數據用該組區間的中點值為代表）.（精確到0.01）
附：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若實數
滿足
，稱為函數
的不動點.有下面三個命題：（1）若是二次函數，且沒有不動點，則函數
也沒有不動點；（2）若是二次函數，則函數可能有
個不動點；（3）若的不動點的個數是
，則的不動點的個數不可能是
；它們中所有真命題的序號是________________________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對定義在
上的函數
和常數
，
，若
恒成立，則稱
為函數的一個“凱森數對”.
（1）若
是的一個“凱森數對”，且
，求
；
（2）已知函數
與
的定義域都為，問它們是否存在“凱森數對”？分別給出判斷并說明理由；
（3）若
是的一個“凱森數對”，且當
時，
，求在區間
上的不動點個數（函數
的不動點即為方程
的解）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C過點M（0，-2）、N（3，1），且圓心C在直線x+2y+1=0上．
（1）求圓C的方程；
（2）設直線ax-y+1=0與圓C交于A，B兩點，是否存在實數a，使得過點P（2，0）的直線l垂直平分弦AB？若存在，求出實數a的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
,若存在區間
,使得
,則稱函數為“可等域函數”,區間A為函數的一個“可等域區間”.給出下列四個函數:①
;②
;③
;④
.其中存在唯一“可等域區間”的“可等域函數”的個數是( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】歐拉公式
（
為虛數單位，
，
為自然底數）是由瑞士著名數學家歐拉發明的，它將指數函數的定義域擴大到復數，建立了三角函數和指數函數的關系，它在復變函數論里占有非重要的地位，被譽為“數學中的天橋”，根據歐拉公式可知，
表示的復數在復平面中位于（ ）
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，已知ABCD為梯形，AB∥CD，CD=2AB，M為線段PC上一點.
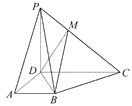
(1)設平面PAB∩平面PDC=l，證明：AB∥l；
(2)在棱PC上是否存在點M，使得PA∥平面MBD，若存在，請確定點M的位置；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知四邊形
的四個頂點在橢圓
： 
上，對角線
所在直線的斜率為
，且
， 
.
（1）當點
為橢圓
的上頂點時，求
所在直線方程；
（2）求四邊形
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
