
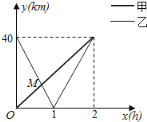
【題目】在一條筆直公路上有A,B兩地,甲騎自行車從A地到B地,乙騎著摩托車從B地到A地,到達A地后立即按原路返回,如圖是甲乙兩人離A地的距離![]() 與行駛時間
與行駛時間![]() 之間的函數圖象,根據圖象解答以下問題:
之間的函數圖象,根據圖象解答以下問題:
![]() 直接寫出
直接寫出![]() ,
,![]() 與x之間的函數關系式
與x之間的函數關系式![]() 不必寫過程
不必寫過程![]() ,求出點M的坐標,并解釋該點坐標所表示的實際意義;
,求出點M的坐標,并解釋該點坐標所表示的實際意義;
![]() 若兩人之間的距離不超過5km時,能夠用無線對講機保持聯系,求在乙返回過程中有多少分鐘甲乙兩人能夠用無線對講機保持聯系;
若兩人之間的距離不超過5km時,能夠用無線對講機保持聯系,求在乙返回過程中有多少分鐘甲乙兩人能夠用無線對講機保持聯系;
![]() 若甲乙兩人離A地的距離之積為
若甲乙兩人離A地的距離之積為![]() ,求出函數
,求出函數![]() 的表達式,并求出它的最大值.
的表達式,并求出它的最大值.
【答案】(1)M(![]() ,
,![]() ),甲乙經過
),甲乙經過![]() h第一次相遇,此時離A距離
h第一次相遇,此時離A距離![]() km;(2)甲乙兩人能夠用無線對講機保持聯系;(3)可得f(x)的最大值為f(2)=1600.
km;(2)甲乙兩人能夠用無線對講機保持聯系;(3)可得f(x)的最大值為f(2)=1600.
【解析】
試題(1)由圖形,結合一次函數的解析式的求法,可得所求解析式;再令y甲=y乙,求得M的坐標,進而得到幾何意義;
(2)令y甲﹣y乙≤5,解不等式可得x的范圍,進而得到所求結論;
(3)運用分段函數的形式寫出f(x),再由二次函數的最值的求法,即可得到所求的最大值.
解:(1)y甲=20x,0≤x≤2;y乙=![]() ,
,
令y甲=y乙,可得20x=40﹣40x,解得x=![]() ,
,
進而y甲=y乙=![]() ,即有M(
,即有M(![]() ,
,![]() ),
),
M的坐標表示:甲乙經過![]() h第一次相遇,此時離A距離
h第一次相遇,此時離A距離![]() km;
km;
(2)乙返回過程中,當1<x≤2時,乙與甲相距5km之內,
即y甲﹣y乙≤5,即為20x﹣(40x﹣40)≤5,解得x≥![]() ,即
,即![]() ≤x≤2,
≤x≤2,
則(2﹣![]() )×60=15分鐘,甲乙兩人能夠用無線對講機保持聯系;
)×60=15分鐘,甲乙兩人能夠用無線對講機保持聯系;
(3)f(x)=![]() =
=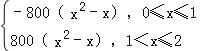
=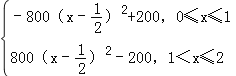 ,
,
當0<x≤1時,f(x)的最大值為f(![]() )=200;
)=200;
當1<x≤2時,f(x)遞增,f(2)為最大值,且為1600.
綜上可得f(x)的最大值為f(2)=1600.


科目:高中數學 來源: 題型:
【題目】某輪船公司的一艘輪船每小時花費的燃料費與輪船航行速度的平方成正比,比例系數為![]() 輪船的最大速度為15海里
輪船的最大速度為15海里![]() 小時
小時![]() 當船速為10海里
當船速為10海里![]() 小時,它的燃料費是每小時96元,其余航行運作費用(不論速度如何)總計是每小時150元
小時,它的燃料費是每小時96元,其余航行運作費用(不論速度如何)總計是每小時150元![]() 假定運行過程中輪船以速度v勻速航行.
假定運行過程中輪船以速度v勻速航行.
![]() 求k的值;
求k的值;
![]() 求該輪船航行100海里的總費用
求該輪船航行100海里的總費用![]() 燃料費
燃料費![]() 航行運作費用
航行運作費用![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=ex+2x2-3x.
(1)求證:函數f (x)在區間[0,1]上存在唯一的極值點.
(2)當x≥![]() 時,若關于x的不等式f (x)≥
時,若關于x的不等式f (x)≥![]() x2+(a-3)x+1恒成立,試求實數a的取值范圍.
x2+(a-3)x+1恒成立,試求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)令![]() ,可將已知三角函數關系
,可將已知三角函數關系![]() 轉換成代數函數關系
轉換成代數函數關系![]() ,試寫出函數
,試寫出函數![]() 的解析式及定義域;
的解析式及定義域;
(2)求函數![]() 的最大值;
的最大值;
(3)函數![]() 在區間
在區間![]() 內是單調函數嗎?若是,請指出其單調性;若不是,請分別指出其單調遞增區間和單調遞減區間(不需要證明).
內是單調函數嗎?若是,請指出其單調性;若不是,請分別指出其單調遞增區間和單調遞減區間(不需要證明).
(參考公式:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)= ![]() ,g(x)=|x﹣2|,則下列結論正確的是( )
,g(x)=|x﹣2|,則下列結論正確的是( )
A.h(x)=f(x)+g(x)是偶函數
B.h(x)=f(x)?g(x)是奇函數
C.h(x)= ![]() 是偶函數
是偶函數
D.h(x)= ![]() 是奇函數
是奇函數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】重慶一中為了增強學生的記憶力和辨識力,組織了一場類似《最強大腦》的![]() 賽,
賽,![]() 兩隊各由4名選手組成,每局兩隊各派一名選手
兩隊各由4名選手組成,每局兩隊各派一名選手![]() ,除第三局勝者得2分外,其余各局勝者均得1分,每局的負者得0分.假設每局比賽
,除第三局勝者得2分外,其余各局勝者均得1分,每局的負者得0分.假設每局比賽![]() 隊選手獲勝的概率均為
隊選手獲勝的概率均為![]() ,且各局比賽結果相互獨立,比賽結束時
,且各局比賽結果相互獨立,比賽結束時![]() 隊的得分高于
隊的得分高于![]() 隊的得分的概率為( )
隊的得分的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com