求函數y=loga(x-x2)(a>0,a≠1)的定義域、值域、單調區間.
【答案】
分析:(1)對數的真數大于0,通過x-x
2>0求解函數的定義域.
(2)先求0<x-x
2的范圍,然后按照0<a<1,a>1兩種情況求解.
(3)按照0<a<1,a>1兩種情況討論,先將原函數分解為兩個基本函數,利用復合函數的單調性求解.
解答:解:(1)由x-x要使函數有意義,必須,x-x
2>0得0<x<1,
所以函數y=log
a(x-x
2)的定義域是(0,1)(2分)
(2)因為0<x-x
2=
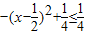
,
所以,當0<a<1時,
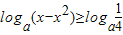
函數y=log
a(x-x
2)的值域為
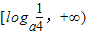
;(5分)
當a>1時,
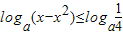
函數y=log
a(x-x
2)的值域為
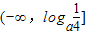
(8分)
(3)當0<a<1時,函數y=log
a(x-x
2)
在
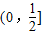
上是減函數,在
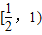
上是增函數;(10分)
當a>1時,函數y=log
a(x-x
2)
在

上是增函數,在
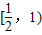
上是減函數.(12分)
點評:本題主要考查:研究復合函數的基本思路,先定義域,再求分解為兩個基本函數,然后利用復合函數的單調性求解.注意分類討論思想的應用.

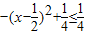 ,
,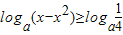
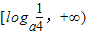 ;(5分)
;(5分)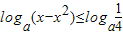
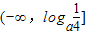 (8分)
(8分)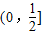 上是減函數,在
上是減函數,在 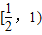 上是增函數;(10分)
上是增函數;(10分) 上是增函數,在
上是增函數,在 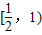 上是減函數.(12分)
上是減函數.(12分)
