

 .
. [
[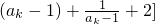
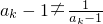 ,
,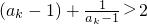 ∴
∴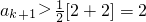 ,
,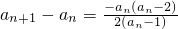
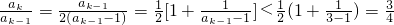
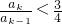 ∴
∴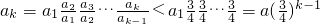
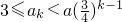 ,
,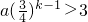 ,
,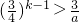
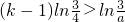 ,又
,又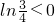 ∴
∴
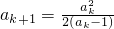 變形為:
變形為: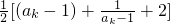 ,然后用上歸納假設ak>2,利用均值不等式可以解答了.
,然后用上歸納假設ak>2,利用均值不等式可以解答了. 推演出
推演出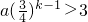 ,那么聯想條件ak≥3,再利用放縮法構造出的ak的關系式來,問題就迎刃而解了.
,那么聯想條件ak≥3,再利用放縮法構造出的ak的關系式來,問題就迎刃而解了.

 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
| 1 |
| 3 |
|
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| (x+1)4+(x-1)4 | (x+1)4-(x-1)4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ) | n |
| N | + |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com