
設數列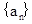 滿足:
滿足: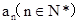 是整數,且
是整數,且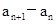 是關于x的方程
是關于x的方程
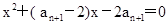 的根.
的根.
(1)若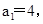 且n≥2時,
且n≥2時,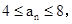 求數列{an}的前100項和S100;
求數列{an}的前100項和S100;
(2)若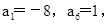 且
且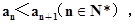 求數列
求數列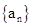 的通項公式.
的通項公式.
(1)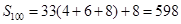 ; (2)
; (2)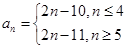 。
。
【解析】
試題分析:(1)由an+1-an是關于x的方程x2+( an+1-2)x-2an+1=0的根,
可得: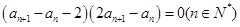 ,
,
所以對一切的正整數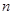 ,
,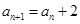 或
或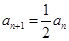 ,
,
若a1=4,且n≥2時,4≤an≤8,則數列{an}為: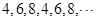
所以,數列{an}的前100項和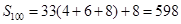 ;
;
(2)若a1=-8,根據an(n∈N*)是整數,an<an+1(n∈N*),且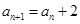 或
或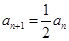
可知,數列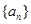 的前6項是:
的前6項是: 或
或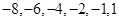 或
或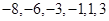 或
或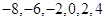 或
或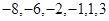
因為a6=1,所以數列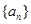 的前6項只能是
的前6項只能是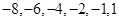 且
且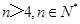 時,
時,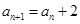 所以,數列{an}的通項公式是:
所以,數列{an}的通項公式是: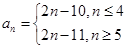
考點:本題主要考查數列的通項公式、求和公式,分段函數的概念。
點評:中檔題,等比數列、等差數列相關內容,已是高考必考內容,其難度飄忽不定,有時突出考查求和問題,如“分組求和法”、“裂項相消法”、“錯位相減法”等,有時則突出涉及數列的證明題。本題解法中,注意通過研究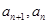 滿足的條件,發現數列特征,確定得到數列的通項公式,帶有普遍性。
滿足的條件,發現數列特征,確定得到數列的通項公式,帶有普遍性。


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源:2012屆上海市崇明中學高三第一學期期中考試試題數學 題型:解答題
(本題滿分18分,第(1)小題4分,第(2)小題6分,第(3)小題8分)
對于數列 ,如果存在一個正整數
,如果存在一個正整數 ,使得對任意的
,使得對任意的 (
( )都有
)都有 成立,那么就把這樣一類數列
成立,那么就把這樣一類數列 稱作周期為
稱作周期為 的周期數列,
的周期數列, 的最小值稱作數列
的最小值稱作數列 的最小正周期,以下簡稱周期。例如當
的最小正周期,以下簡稱周期。例如當 時
時 是周期為
是周期為 的周期數列,當
的周期數列,當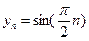 時
時 是周期為
是周期為 的周期數列。
的周期數列。
(1)設數列 滿足
滿足 (
( ),
), (
( 不同時為0),且數列
不同時為0),且數列 是周期為
是周期為 的周期數列,求常數
的周期數列,求常數 的值;
的值;
(2)設數列 的前
的前 項和為
項和為 ,且
,且 .
.
①若 ,試判斷數列
,試判斷數列 是否為周期數列,并說明理由;
是否為周期數列,并說明理由;
②若 ,試判斷數列
,試判斷數列 是否為周期數列,并說明理由;
是否為周期數列,并說明理由;
(3)設數列 滿足
滿足 (
( ),
), ,
,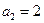 ,
, ,數列
,數列 的前
的前 項和為
項和為 ,試問是否存在
,試問是否存在 ,使對任意的
,使對任意的 都有
都有 成立,若存在,求出
成立,若存在,求出 的取值范圍;不存在, 說明理由;
的取值范圍;不存在, 說明理由;
查看答案和解析>>
科目:高中數學 來源:2013-2014學年江西省新課程高三上學期第三次適應性測試文科數學試卷(解析版) 題型:解答題
已知數列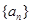 為等差數列,數列
為等差數列,數列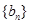 為等比數列且公比大于1,若
為等比數列且公比大于1,若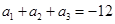 ,
,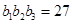 ,且
,且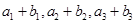 恰好是一各項均為正整數的等比數列的前三項.
恰好是一各項均為正整數的等比數列的前三項.
(1)求數列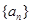 ,
,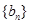 的通項公式;
的通項公式;
(2)設數列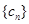 滿足
滿足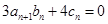
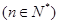 ,求
,求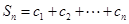 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省名校新高考研究聯盟高三第二次聯考文科數學試卷(解析版) 題型:解答題
.設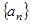 是公差不為零的等差數列,
是公差不為零的等差數列,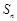 為其前
為其前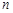 項和,滿足:
項和,滿足: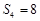 且
且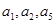 成等比數列.
成等比數列.
(I)求數列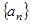 的通項公式;
的通項公式;
(II)設數列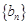 滿足:
滿足: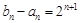 ,
,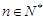 ,
,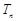 為數列
為數列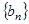 的前
的前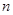 項和,問是否存在正整數
項和,問是否存在正整數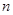 ,使得
,使得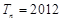 成立?若存在,求出
成立?若存在,求出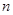 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三下學期開學質量檢測數學試卷 題型:解答題
(本題滿分16分)
對于數列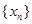 ,如果存在一個正整數
,如果存在一個正整數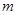 ,使得對任意的
,使得對任意的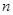 (
(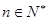 )都有
)都有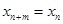 成立,那么就把這樣一類數列
成立,那么就把這樣一類數列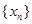 稱作周期為
稱作周期為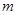 的周期數列,
的周期數列,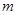 的最小值稱作數列
的最小值稱作數列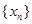 的最小正周期,以下簡稱周期.例如當
的最小正周期,以下簡稱周期.例如當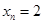 時
時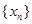 是周期為
是周期為 的周期數列,當
的周期數列,當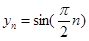 時
時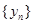 是周期為
是周期為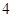 的周期數列.
的周期數列.
(1)設數列 滿足
滿足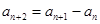 (
(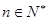 ),
),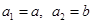 (
(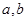 不同時為0),求證:數列
不同時為0),求證:數列 是周期為
是周期為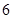 的周期數列,并求數列
的周期數列,并求數列 的前2012項的和
的前2012項的和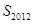 ;
;
(2)設數列 的前
的前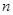 項和為
項和為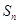 ,且
,且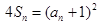 .
.
①若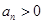 ,試判斷數列
,試判斷數列 是否為周期數列,并說明理由;
是否為周期數列,并說明理由;
②若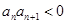 ,試判斷數列
,試判斷數列 是否為周期數列,并說明理由;
是否為周期數列,并說明理由;
(3)設數列 滿足
滿足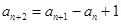 (
(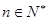 ),
),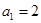 ,
,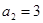 ,數列
,數列 的前
的前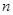 項和為
項和為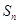 ,試問是否存在實數
,試問是否存在實數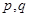 ,使對任意的
,使對任意的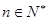 都有
都有 成立,若存在,求出
成立,若存在,求出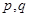 的取值范圍;不存在,說明理由.
的取值范圍;不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com