
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調區間;
的單調區間;
(2)若![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)證明:![]() .
.
【答案】(1)分類討論,詳見解析;(2)![]() ;(3)詳見解析.
;(3)詳見解析.
【解析】
(1)對函數![]() 求導,再根據
求導,再根據![]() 的正負分類討論單調性即可;
的正負分類討論單調性即可;
(2)解法一:若![]() 恒成立,即
恒成立,即![]() ,根據(1)中
,根據(1)中![]() 的單調性求出其最大值即可列式求解;解法二:若
的單調性求出其最大值即可列式求解;解法二:若![]() 恒成立,即
恒成立,即![]() 恒成立,構造函數
恒成立,構造函數![]() ,利用導數求出其最大值即可得出結論;
,利用導數求出其最大值即可得出結論;
(3)由(2)知當![]() 時,有
時,有![]() 在
在![]() 恒成立,令
恒成立,令![]() ,即可推出
,即可推出![]() ,再對不等式兩邊累加求和,即可推出結論.
,再對不等式兩邊累加求和,即可推出結論.
(1)函數![]() 的定義域為
的定義域為![]() ,
,![]() ,
,
①當![]() 時,
時,![]() ,則
,則![]() 在
在![]() 上是增函數;
上是增函數;
②當![]() 時,由
時,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
則![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
(2)解法一:
由(1)知![]() 時,
時,![]() 在
在![]() 遞增,而
遞增,而![]() ,
,
所以![]() 不恒成立,故
不恒成立,故![]() ,
,
又由(1)知![]() 時
時![]() ,
,
因為![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() ,
,
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
解法二:
由題意知![]() ,因為
,因為![]() 恒成立,所以
恒成立,所以![]() 恒成立,
恒成立,
令![]() ,則
,則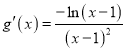 ,
,
令![]() ,令
,令![]() ,
,
所以![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
所以![]() ,
,
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
(3)由(2)知,當![]() 時,有
時,有![]() 在
在![]() 恒成立,
恒成立,
令![]() ,則
,則![]() ,
,
即![]() ,從而
,從而![]() ,
,
所以![]() ,
,
即![]() .
.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】將2、3、4、6、8、9、12、15共八個數排成一行,使得任意相鄰兩個數的最大公約數均大于1.則所有可能的排法共有()種
A. 720 B. 1014 C. 576 D. 1296
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知直線![]() 與圓O:
與圓O:![]() 相切.
相切.
(1)直線l過點(2,1)且截圓O所得的弦長為![]() ,求直線l的方程;
,求直線l的方程;
(2)已知直線y=3與圓O交于A,B兩點,P是圓上異于A,B的任意一點,且直線AP,BP與y軸相交于M,N點.判斷點M、N的縱坐標之積是否為定值?若是,求出該定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A,B,C是一條直線道路上的三點,![]() .從A,B,C三點分別遙望電視塔M,在點A見塔在東北方向,在點B見塔在正東方向,在點C見塔在南偏東
.從A,B,C三點分別遙望電視塔M,在點A見塔在東北方向,在點B見塔在正東方向,在點C見塔在南偏東![]() ,求塔與這條道路的最短距離(精確到0.1km).
,求塔與這條道路的最短距離(精確到0.1km).
查看答案和解析>>
科目:高中數學 來源: 題型:
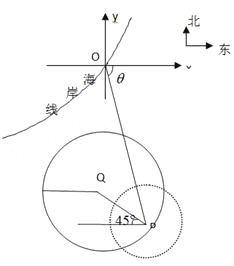
【題目】在某海濱城市附近海面有一臺風,據監測,當前臺風中心位于城市O(如圖)的東偏南![]() 方向300km的海面P處,并以20km/h的速度向西偏北
方向300km的海面P處,并以20km/h的速度向西偏北![]() 方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60km,并以10km/h的速度不斷增大,問幾小時后該城市開始受到臺風的侵襲?
方向移動,臺風侵襲的范圍為圓形區域,當前半徑為60km,并以10km/h的速度不斷增大,問幾小時后該城市開始受到臺風的侵襲?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,三棱柱![]() 中,側棱
中,側棱![]() 垂直底面,∠ACB=90°,
垂直底面,∠ACB=90°,![]() ,D為
,D為![]() 的中點,點P為AB的中點.
的中點,點P為AB的中點.

(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() ;
;
(3)求三棱錐B-CDP的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com