
【題目】設![]() 是公比為正整數的等比數列,
是公比為正整數的等比數列,![]() 是等差數列,且
是等差數列,且![]() ,
,![]() ,
,![]() .
.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)設 數列
數列![]() 的前
的前![]() 項和為
項和為![]() .
.
①試求最小的正整數![]() ,使得當
,使得當![]() 時,都有
時,都有![]() 成立;
成立;
②是否存在正整數![]()
![]() ,使得
,使得![]() 成立?若存在,請求出所有滿足條件的
成立?若存在,請求出所有滿足條件的![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
【答案】(1)![]() ;
;
(2)①最小的正整數![]() ;②存在正整數
;②存在正整數![]() ,使得
,使得![]() 成立.
成立.
【解析】
試題分析:
(1)利用等差數列與等比數列的通項公式即可得出;(2)①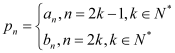 ,
,
可得數列![]() 的前2n項和
的前2n項和![]() ,設
,設![]() ,則
,則![]() ,
,![]() 時,
時,![]() ,即
,即![]() 時,
時,![]() ,數列
,數列![]() 在
在![]() 時單調遞增,而
時單調遞增,而![]() ,所以
,所以![]() ,即可得出最小的正整數.②由
,即可得出最小的正整數.②由![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .按
.按![]() 的奇偶性分情況: 1°當
的奇偶性分情況: 1°當![]() 同時為偶數時,由①可知
同時為偶數時,由①可知![]() ; 2°當
; 2°當![]() 同時為奇數時,
同時為奇數時,![]() 時,
時,![]() ,數列
,數列![]() 在
在![]() 時單調遞增,
時單調遞增,![]() 不成立; 3°當
不成立; 3°當![]() 為偶數,
為偶數,![]() 為奇數時,
為奇數時,![]() ,
,![]() 不成立; 4°當
不成立; 4°當![]() 為奇數,
為奇數,![]() 為偶數時,顯然
為偶數時,顯然![]() 時,
時,![]() 不成立;綜合即可得出使得
不成立;綜合即可得出使得![]() 成立的正整數
成立的正整數![]() .
.
試題解析:
(1)由![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
設![]() 的公比為
的公比為![]() ,
,![]() 的公差為
的公差為![]() ,
,
由![]() ,
,
得![]() ,
,
即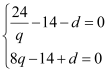 ,消去
,消去![]() ,得
,得![]() ,
,
解得![]() 或
或![]() ,
,
又![]() ,
,
![]() ,
,
得![]() .
.
(2)①![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
設![]() ,
,
則![]() ,
,
![]()
所以數列![]() 單調遞增,則
單調遞增,則![]() 時,
時,![]() ,
,
即![]() 時,
時,![]() ,數列
,數列![]() 在
在![]() 時單調遞增,
時單調遞增,
而![]() ,所以當
,所以當![]() 時,
時,![]() ,
,
綜上,最小的正整數![]() .
.
②法一:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
1.當![]() 同時為偶數時,由①可知
同時為偶數時,由①可知![]() ;
;
2.當![]() 同時為奇數時,設
同時為奇數時,設![]() ,
,
則![]() ,
,
![]()
所以數列![]() 單調遞增,則當
單調遞增,則當![]() 時,
時,![]() ,
,
即![]() 時,
時,![]() ,數列
,數列![]() 在
在![]() 時單調遞增,
時單調遞增,
而![]() ,
,
故當![]() 同時為奇數時,
同時為奇數時,![]() 不成立;
不成立;
3.當![]() 為偶數,
為偶數,![]() 為奇數時,顯然
為奇數時,顯然![]() 時,
時,![]() 不成立,
不成立,
若![]() ,則
,則![]() ,
,
![]() ,
,![]() ,
,
由2.可知![]() ,
,![]() ,
,
![]() 當
當![]() 為偶數,
為偶數,![]() 為奇數時,
為奇數時,![]() 不成立;
不成立;
4.當![]() 為奇數,
為奇數,![]() 為偶數時,顯然
為偶數時,顯然![]() 時,
時,![]() 不成立,
不成立,
若![]() ,則
,則![]() ,
,
若![]() ,
,
則![]() ,
,
即![]() ,
,![]() 時,
時,![]() 不成立,
不成立,
若![]() ,即
,即![]() ,
,
由①中數列![]() 的單調性,可知
的單調性,可知![]() ,
,

設![]() ,
,
![]() 恒成立,
恒成立,
所以數列![]() 單調遞增,
單調遞增,
則當![]() 時,
時,![]() ,
,
![]() ,
,
![]() 時
時![]() 也不成立;
也不成立;
綜上1.2.3.4.,存在正整數![]() ,使得
,使得![]() 成立.
成立.
法二:可以證明當![]() 時,不等式
時,不等式![]() 恒成立,余下略.
恒成立,余下略.


科目:高中數學 來源: 題型:
【題目】總體有編號為01,02,…,19,20的20個個體組成。利用下面的隨機數表選取6個個體,選取方法是從隨機數表第1行的第5列和第6列數字開始由左到右依次選取兩個數字,則選出來的第6個個體的編號為( )
7816 6572 0802 6314 0702 4369 9728 0198 |
3204 9234 4935 8200 3623 4869 6938 7481 |
A. 14 B. 07 C. 04 D. 01
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地干旱少雨,農作物受災嚴重,為了使今后保證農田灌溉,當地政府決定建一橫斷面為等腰梯形的水渠(水渠的橫斷面如圖所示),為減少水的流失量,必須減少水與渠壁的接觸面,若水渠橫斷面的面積設計為定值S,渠深為h,則水渠壁的傾斜角α(0<α<![]() )為多大時,水渠中水的流失量最小?
)為多大時,水渠中水的流失量最小?
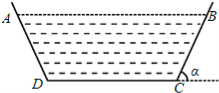
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解籃球愛好者小李的投籃命中率與打籃球時間的關系,下表記錄了小李某月連續5天每天打籃球時間![]() (單位:小時)與當天投籃命中率
(單位:小時)與當天投籃命中率![]() 之間的關系:
之間的關系:
時間 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(Ⅰ)請根據上表提供的數據,用最小二乘法求出投籃命中率![]() 與打籃球時間
與打籃球時間![]() (單位:小時)之間的回歸直線方程
(單位:小時)之間的回歸直線方程![]() ;
;
(Ⅱ)如果小李某天打了2.5小時籃球,預測小李當天的投籃命中率.
(參考:用最小二乘法求線性回歸方程系數公式 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某大學一年級女生中,選取身高分別是150cm、155cm、160cm、165cm、170cm的學生各一名,其身高和體重數據如表所示:
身高/cm ( | 150 | 155 | 160 | 165 | 170 |
體重/kg ( | 43 | 46 | 49 | 51 | 56 |
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)利用(1)中的回歸方程,計算身高為168cm時,體重的估計值![]() 為多少?
為多少?
參考公式:線性回歸方程![]() ,其中
,其中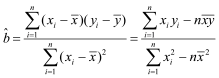 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校高中畢業班有男生![]() 人,女生
人,女生![]() 人,學校為了對高三學生數學學習情況進行分析,從高三年級按照性別進行分層抽樣,抽取
人,學校為了對高三學生數學學習情況進行分析,從高三年級按照性別進行分層抽樣,抽取![]() 名學生成績,統計數據如下表所示:
名學生成績,統計數據如下表所示:
分數段(分) |
|
|
|
|
| 總計 |
頻數 |
|
|
|
|
|
|
(1)若成績在![]() 分以上(含
分以上(含![]() 分),則成績為及格,請估計該校畢業班平均成績和及格學生人數;
分),則成績為及格,請估計該校畢業班平均成績和及格學生人數;
(2)如果樣本數據中,有60名女生數學成績及格,請完成如下數學成績與性別的列聯表,并判斷是否有![]() 的把握認為:“該校學生的數學成績與性別有關”.
的把握認為:“該校學生的數學成績與性別有關”.
女生 | 男生 | 總計 | |
及格人數 |
| ||
不及格人數 | |||
總計 |
參考公式:![]()
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知極坐標的極點在平面直角坐標系的原點![]() 處,極軸與
處,極軸與![]() 軸的正半軸重合,且長度單位相同。
軸的正半軸重合,且長度單位相同。
直線![]() 的極坐標方程為:
的極坐標方程為: ,點
,點![]() ,參數
,參數![]() 。
。
(1)求點![]() 軌跡的直角坐標方程;
軌跡的直角坐標方程;
(2)求點![]() 到直線
到直線![]() 距離的最大值。
距離的最大值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com