【題目】已知△ABC的內角A，B，C的對邊分別為a，b，c．
（1）若
的面積
，求a+c值；
（2）若2cosC（
+
）=c2，求角C．
【答案】（1）5（2）
【解析】
（1）由已知利用三角形面積公式可求ac=6，結合余弦定理可求a+c的值．
（2）利用平面向量數量積的運算，正弦定理，三角函數恒等變換的應用化簡已知等式可求cosC=
，結合范圍C∈（0，π），可求C的值．
解：（1）∵
的面積
，
∴
=
acsinB=
ac，可得：ac=6，
∵由余弦定理b2=a2+c2-2accosB，可得：7=a2+c2-ac=（a+c）2-3ac=（a+c）2-18，
解得：a+c=5．
（2）∵2cosC（
+
）=c2，
∴2cosC（accosB+bccosA）=c2，可得：2cosC（acosB+bcosA）=c，
∴由正弦定理可得：2cosC（sinAcosB+sinBcosA）=sinC，即2cosCsinC=sinC，
∵sinC≠0，
∴cosC=，
∵C∈（0，π），
∴C=．
科目：高中數學 來源： 題型：
【題目】已知函數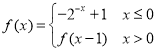
,則下列命題中正確命題的個數是（ ）
①函數
在
上為周期函數
②函數在區間
,
上單調遞增
③函數在
（
）取到最大值
,且無最小值
④若方程
（
）有且僅有兩個不同的實根,則
A.
個B.
個C.
個D.
個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知正三棱錐P-ABC的側面是直角三角形，PA=6，頂點P在平面ABC內的正投影為點D，D在平面PAB內的正投影為點E，連結PE并延長交AB于點G.
（Ⅰ）證明：G是AB的中點；
（Ⅱ）在圖中作出點E在平面PAC內的正投影F（說明作法及理由），并求四面體PDEF的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某學校研究性課題《什么樣的活動最能促進同學們進行垃圾分類》向題的統計圖（每個受訪者都只能在問卷的5個活動中選擇一個），以下結論錯誤的是（ ）
A. 回答該問卷的總人數不可能是100個
B. 回答該問卷的受訪者中，選擇“設置分類明確的垃圾桶”的人數最多
C. 回答該問卷的受訪者中，選擇“學校團委會宣傳”的人數最少
D. 回答該問卷的受訪者中，選擇“公益廣告”的人數比選擇“學校要求”的少8個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
在橢圓
上，
為坐標原點，直線
的斜率與直線
的斜率乘積為
.
（1）求橢圓
的方程；
（2）不經過點
的直線
（
且
）與橢圓交于
，
兩點，關于原點的對稱點為
（與點不重合），直線
，
與
軸分別交于兩點
，
，求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
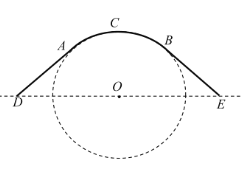
【題目】某公園為了美化環境和方便顧客，計劃建造一座圓弧形拱橋，已知該橋的剖面如圖所示，共包括圓弧形橋面
和兩條長度相等的直線型路面
、
，橋面跨度
的長不超過
米，拱橋所在圓的半徑為
米，圓心
在水面上，且和所在直線與圓分別在連結點
和
處相切.設
，已知直線型橋面每米修建費用是
元，弧形橋面每米修建費用是
元.
（1）若橋面（線段、和弧）的修建總費用為
元，求關于
的函數關系式；
（2）當為何值時，橋面修建總費用最低？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的質量以其質量指標值衡量，并依據質量指標值劃分等級如下表：
從某企業生產的這種產品中抽取200件，檢測后得到如下的頻率分布直方圖：
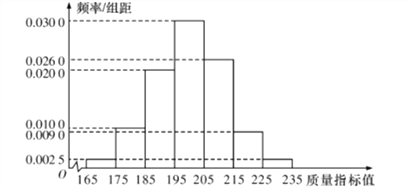
(1)根據以上抽樣調查數據，能否認為該企業生產的這種產品符合“一、二等品至少要占全部產品
”的規定？
(2)在樣本中，按產品等級用分層抽樣的方法抽取8件，再從這8件產品中隨機抽取4件，求抽取的4件產品中，一、二、三等品都有的概率；
(3)該企業為提高產品質量，開展了“質量提升月”活動，活動后再抽樣檢測，產品質量指標值
近似滿足
，則“質量提升月”活動后的質量指標值的均值比活動前大約提升了多少？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
