
【題目】一個(gè)創(chuàng)業(yè)青年租用一塊邊長為4百米的等邊![]() 田地
田地![]() 如圖
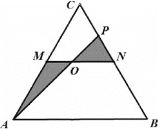
如圖![]() 養(yǎng)蜂、產(chǎn)蜜與售蜜,田地內(nèi)擬修建筆直小路MN,AP,其中M,N分別為AC,BC的中點(diǎn),點(diǎn)P在CN上,
養(yǎng)蜂、產(chǎn)蜜與售蜜,田地內(nèi)擬修建筆直小路MN,AP,其中M,N分別為AC,BC的中點(diǎn),點(diǎn)P在CN上,![]() 規(guī)劃在小路MN與AP的交點(diǎn)O(O與M、N不重合
規(guī)劃在小路MN與AP的交點(diǎn)O(O與M、N不重合![]() 處設(shè)立售蜜點(diǎn),圖中陰影部分為蜂巢區(qū),空白部分為蜂源植物生長區(qū),A,N為出入口
處設(shè)立售蜜點(diǎn),圖中陰影部分為蜂巢區(qū),空白部分為蜂源植物生長區(qū),A,N為出入口![]() 小路的寬度不計(jì)
小路的寬度不計(jì)![]() 為節(jié)約資金,小路MO段與OP段建便道,供蜂源植物培育之用,費(fèi)用忽略不計(jì)
為節(jié)約資金,小路MO段與OP段建便道,供蜂源植物培育之用,費(fèi)用忽略不計(jì)![]() 為車輛安全出入,小路AO段的建造費(fèi)用為每百米5萬元,小路ON段的建造費(fèi)用為每百米4萬元.
為車輛安全出入,小路AO段的建造費(fèi)用為每百米5萬元,小路ON段的建造費(fèi)用為每百米4萬元.
(Ⅰ)若擬修的小路AO段長為![]() 百米,求小路ON段的建造費(fèi)用;
百米,求小路ON段的建造費(fèi)用;
(Ⅱ)設(shè)![]() , 求
, 求![]() 的值,使得小路AO段與ON段的建造總費(fèi)用最小.
的值,使得小路AO段與ON段的建造總費(fèi)用最小.
【答案】(Ⅰ)4萬元;(Ⅱ)![]() ,小路AO段與ON段的建造總費(fèi)用最小為
,小路AO段與ON段的建造總費(fèi)用最小為![]() 萬元.
萬元.
【解析】
(Ⅰ)在![]() 中用余弦定理計(jì)算
中用余弦定理計(jì)算![]() 的長度,故可得
的長度,故可得![]() 的長度后即得
的長度后即得![]() 段的建筑費(fèi)用.
段的建筑費(fèi)用.
(Ⅱ)在![]() 中用正弦定理計(jì)算
中用正弦定理計(jì)算![]() 的長度后得到
的長度后得到![]() ,令
,令![]() ,將其變形為
,將其變形為![]() ,利用輔助角公式可得
,利用輔助角公式可得![]() ,從而得到
,從而得到![]() ,驗(yàn)證等號成立后可得何時(shí)取最小值.
,驗(yàn)證等號成立后可得何時(shí)取最小值.
(Ⅰ)在![]() 中,
中,![]() ,
,
![]() 即
即![]() ,
,
故![]() 或
或![]() (舎去),故
(舎去),故![]() ,
,
所以![]() 段的建筑費(fèi)用為
段的建筑費(fèi)用為![]() 萬元.
萬元.
(Ⅱ)由正弦定理得:在![]() 中,
中,![]() ,
,
故![]() ,
,
![]()
設(shè)小路![]() 和
和![]() 段的建造總費(fèi)用為
段的建造總費(fèi)用為![]() ,
,
則![]() ,
,
令![]() ,且
,且![]() ,
,![]() ,
,
![]() 即
即![]() .
.
由![]() ,得
,得![]() ,故
,故![]() ,即
,即![]() 或
或![]() (舍去).
(舍去).
當(dāng)![]() 時(shí),
時(shí),![]() ,故
,故![]() ,其中
,其中![]() ,
,
故由![]() ,符合題意.
,符合題意.
答:![]() ,小路AO段與ON段的建造總費(fèi)用最小為
,小路AO段與ON段的建造總費(fèi)用最小為![]() 萬元.
萬元.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)P是橢圓![]() 上一點(diǎn),M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點(diǎn),則|PM|+|PN|的最小值、最大值分別為 ( )
上一點(diǎn),M,N分別是兩圓(x+4)2+y2=1和(x-4)2+y2=1上的點(diǎn),則|PM|+|PN|的最小值、最大值分別為 ( )
A. 9,12 B. 8,11 C. 10,12 D. 8,12
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)已知兩個(gè)變量線性相關(guān),若它們的相關(guān)性越強(qiáng),則相關(guān)系數(shù)的絕對值越接近于1.
(2)線性回歸直線必過點(diǎn)![]() ;
;
(3)對于分類變量A與B的隨機(jī)變量![]() ,
,![]() 越大說明“A與B有關(guān)系”的可信度越大.
越大說明“A與B有關(guān)系”的可信度越大.
(4)在刻畫回歸模型的擬合效果時(shí),殘差平方和越小,相關(guān)指數(shù)![]() 的值越大,說明擬合的效果越好.
的值越大,說明擬合的效果越好.
(5)根據(jù)最小二乘法由一組樣本點(diǎn)![]() ,求得的回歸方程是
,求得的回歸方程是![]() ,對所有的解釋變量
,對所有的解釋變量![]() ,
,![]() 的值一定與
的值一定與![]() 有誤差.
有誤差.
以上命題正確的序號為____________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在底面是菱形的四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,且
上,且![]() .
.
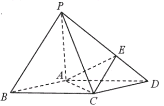
(1)證明:![]() 面
面![]() ;
;
(2)在棱![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn)![]() ,使三棱錐
,使三棱錐![]() 是正三棱錐?證明你的結(jié)論.
是正三棱錐?證明你的結(jié)論.
(3)求以![]() 為棱,
為棱,![]() 與
與![]() 為面的二面角
為面的二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某工廠對一批產(chǎn)品進(jìn)行了抽樣檢測.右圖是根據(jù)抽樣檢測后的產(chǎn)品凈重(單位:克)數(shù)據(jù)繪制的頻率分布直方圖,其中產(chǎn)品凈重的范圍是[96,106],樣本數(shù)據(jù)分組為[96,98),[98,100),[100,102),[102,104),[104,106],已知樣本中產(chǎn)品凈重小于100克的個(gè)數(shù)是36,則樣本中凈重大于或等于98克并且小于104克的產(chǎn)品的個(gè)數(shù)是( ).
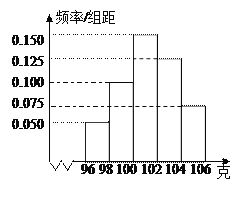
A. 90B. 75C. 60D. 45
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過拋物線![]() (其中
(其中![]() )的焦點(diǎn)
)的焦點(diǎn)![]() 的直線交拋物線于
的直線交拋物線于![]() 兩點(diǎn),且
兩點(diǎn),且![]() 兩點(diǎn)的縱坐標(biāo)之積為
兩點(diǎn)的縱坐標(biāo)之積為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)當(dāng)![]() 時(shí),求
時(shí),求![]() 的值;
的值;
(3)對于![]() 軸上給定的點(diǎn)
軸上給定的點(diǎn)![]() (其中
(其中![]() ),若過點(diǎn)
),若過點(diǎn)![]() 和
和![]() 兩點(diǎn)的直線交拋物線
兩點(diǎn)的直線交拋物線![]() 的準(zhǔn)線
的準(zhǔn)線![]() 點(diǎn),求證:直線
點(diǎn),求證:直線![]() 與
與![]() 軸交于一定點(diǎn).
軸交于一定點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知橢圓![]() ,直線
,直線![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸對稱,直線
軸對稱,直線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.

(1)若點(diǎn)![]() 是橢圓
是橢圓![]() 的一個(gè)焦點(diǎn),求該橢圓的長軸的長度;
的一個(gè)焦點(diǎn),求該橢圓的長軸的長度;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 在
在![]() 時(shí)取得極值,求實(shí)數(shù)
時(shí)取得極值,求實(shí)數(shù)![]() 的值;
的值;
(Ⅱ)當(dāng)![]() 時(shí),求
時(shí),求![]() 零點(diǎn)的個(gè)數(shù).
零點(diǎn)的個(gè)數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《九章算術(shù)》是中國古代第一部數(shù)學(xué)專著,全書總結(jié)了戰(zhàn)國、秦、漢時(shí)期的數(shù)學(xué)成就。“更相減損術(shù)”便出自其中,原文記載如下:“可半者半之,不可半者,副置分母、子之?dāng)?shù),以少減多,更相減損,求其等也。”其核心思想編譯成如示框圖,若輸入的![]() ,
,![]() 分別為45,63,則輸出的
分別為45,63,則輸出的![]() 為( )
為( )
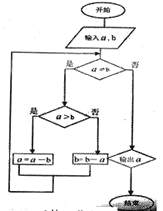
A. 2B. 3C. 5D. 9
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com