
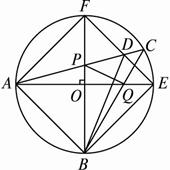
圖2-2-12
思路分析:由已知條件可以證明四邊形ABEF是正方形,且邊長為![]() ,則正方形面積為2.而△ABD的面積為正方形面積的一半,所以,只需證明S四邊形APQB =S△ABD,即證S△BPD?=S△BPQ?,即證DQ∥PB.因為BP⊥AE,所以,只需證DQ⊥AE.
,則正方形面積為2.而△ABD的面積為正方形面積的一半,所以,只需證明S四邊形APQB =S△ABD,即證S△BPD?=S△BPQ?,即證DQ∥PB.因為BP⊥AE,所以,只需證DQ⊥AE.
證明:∵AE、BF為互相垂直的兩條直徑,垂足O為圓心,?
∴AE、BF互相平分、垂直且相等.∴四邊形ABEF是正方形.?
∴∠ACB =∠AEF =45°,即∠DCQ =∠QED.?
∴D、Q、E、C四點共圓.連結CE、DQ,則∠DCE +∠DQE =180°.?
∵AE為⊙O的直徑,∴∠DCE =90°,∠DQE =90°.?
∵∠FOE =90°,進而DQ∥BF,∴S△BPQ =S△BPD?,?
∴S△ABP +S△BPQ =S△ABP +S△BPD,即S四邊形ABQP =S△ABD.?
∵⊙O的半徑為1,∴正方形邊長為![]() ,即AB =AF =
,即AB =AF =![]() .?
.?
∴S四邊形ABQP =S△ABD?=![]() AB·AF =1.
AB·AF =1.


科目:高中數學 來源: 題型:

圖1-2-13
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com