
(本小題滿分14分)
設 橢圓方程為
橢圓方程為 拋物線方程為
拋物線方程為 如圖4所示,過點
如圖4所示,過點 作
作 軸的平行線,與拋物線在第一象限的交點為G.已知拋物線在點G的切線經過橢圓的右焦點
軸的平行線,與拋物線在第一象限的交點為G.已知拋物線在點G的切線經過橢圓的右焦點
(1)求滿足條件的橢圓方程和拋物線方程;
(2)設A,B分別是橢圓長軸的左、右端點,試探究在拋物線上是否存在點P,使得 為直角三角形?若存在,請指出共有幾個這樣的點?并說明理由(不必具體求出這些點的坐標) 。
為直角三角形?若存在,請指出共有幾個這樣的點?并說明理由(不必具體求出這些點的坐標) 。

(1)橢圓和拋物線的方程分別為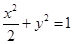 和
和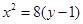 ;
;
(2)存在,有4個點,理由見解析。
【解析】 對于(1)重點要抓住拋物線在點G的切線經過橢圓的右焦點F1,故先要設法求出點G及拋物線在點G的切線,再求F1,利用同一個F1求出b即可;對于(2)首先要注意直角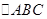 三個角均有可能為直角,不要遺漏,對于
三個角均有可能為直角,不要遺漏,對于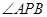 為直角的情況可利用向量或斜率求解;
為直角的情況可利用向量或斜率求解;
(1)由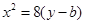 得
得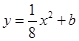 ,
,
當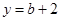 得
得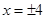 ,
,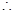 G點的坐標為
G點的坐標為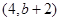 ,
,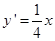 ,
,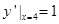 ,
,
過點G的切線方程為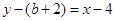 即
即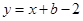 ,
,
令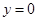 得
得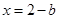 ,
,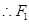 點的坐標為
點的坐標為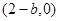 ,由橢圓方程得
,由橢圓方程得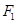 點的坐標為
點的坐標為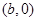 ,
,
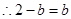 即
即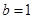 ,
,
即橢圓和拋物線的方程分別為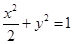 和
和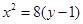 ;
;
(2)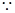 過
過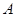 作
作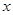 軸的垂線與拋物線只有一個交點
軸的垂線與拋物線只有一個交點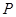 ,
,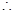 以
以 為直角的
為直角的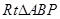 只有一個,同理
只有一個,同理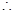 以
以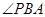 為直角的
為直角的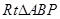 只有一個。
只有一個。
若以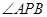 為直角,設
為直角,設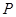 點坐標為
點坐標為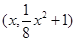 ,
,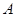 、
、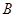 兩點的坐標分別為
兩點的坐標分別為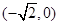 和
和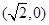 ,
, 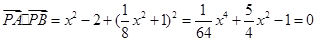 。
。
關于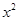 的二次方程有一解,
的二次方程有一解,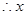 有兩解,即以
有兩解,即以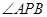 為直角的
為直角的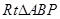 有兩個,因此拋物線上存在四個點使得
有兩個,因此拋物線上存在四個點使得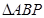 為直角三角形。
為直角三角形。


 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:高中數學 來源: 題型:
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)設橢圓C1的方程為![]() (a>b>0),曲線C2的方程為y=
(a>b>0),曲線C2的方程為y=![]() ,且曲線C1與C2在第一象限內只有一個公共點P。(1)試用a表示點P的坐標;(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式。
,且曲線C1與C2在第一象限內只有一個公共點P。(1)試用a表示點P的坐標;(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式。
查看答案和解析>>
科目:高中數學 來源:2011年江西省撫州市教研室高二上學期期末數學理卷(A) 題型:解答題
(本小題滿分14分)
已知 =2,點(
=2,點( )在函數
)在函數 的圖像上,其中
的圖像上,其中 =
= .
.
(1)證明:數列 }是等比數列;
}是等比數列;
(2)設 ,求
,求 及數列{
及數列{ }的通項公式;
}的通項公式;
(3)記 ,求數列{
,求數列{ }的前n項和
}的前n項和 ,并證明
,并證明 .
.
查看答案和解析>>
科目:高中數學 來源:2015屆山東省威海市高一上學期期末考試數學試卷(解析版) 題型:解答題
(本小題滿分14分)
某網店對一應季商品過去20天的銷售價格及銷售量進行了監測統計發現,第 天(
天( )的銷售價格(單位:元)為
)的銷售價格(單位:元)為 ,第
,第 天的銷售量為
天的銷售量為 ,已知該商品成本為每件25元.
,已知該商品成本為每件25元.
(Ⅰ)寫出銷售額 關于第
關于第 天的函數關系式;
天的函數關系式;
(Ⅱ)求該商品第7天的利潤;
(Ⅲ)該商品第幾天的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省高三下學期第一次月考文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)已知 的圖像在點
的圖像在點 處的切線與直線
處的切線與直線 平行.
平行.
⑴ 求 ,
, 滿足的關系式;
滿足的關系式;
⑵ 若 上恒成立,求
上恒成立,求 的取值范圍;
的取值范圍;
⑶ 證明: (
( )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com