
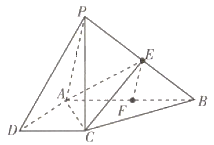
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,四邊形
,四邊形![]() 是直角梯形,
是直角梯形,![]() ,F是
,F是![]() 的中點,E是
的中點,E是![]() 上的一點,則下列說法正確的是( )
上的一點,則下列說法正確的是( )
A.若![]() ,則
,則![]() 平面
平面![]()
B.若![]() ,則四棱錐
,則四棱錐![]() 的體積是三棱錐
的體積是三棱錐![]() 體積的6倍
體積的6倍
C.三棱錐![]() 中有且只有三個面是直角三角形
中有且只有三個面是直角三角形
D.平面![]() 平面
平面![]()
【答案】AD
【解析】
利用中位線的性質即可判斷選項A;先求得四棱錐![]() 的體積與四棱錐
的體積與四棱錐![]() 的體積的關系,再由四棱錐
的體積的關系,再由四棱錐![]() 的體積與三棱錐
的體積與三棱錐![]() 的關系進而判斷選項B;由線面垂直的性質及勾股定理判斷選項C;先證明
的關系進而判斷選項B;由線面垂直的性質及勾股定理判斷選項C;先證明![]() 平面
平面![]() ,進而證明平面
,進而證明平面![]() 平面
平面![]() ,即可判斷選項D.
,即可判斷選項D.
對于選項A,因為![]() ,所以
,所以![]() 是
是![]() 的中點,
的中點,
因為F是![]() 的中點,所以
的中點,所以![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故A正確;
,故A正確;
對于選項B,因為![]() ,所以
,所以![]() ,
,
因為![]() ,
,
所以梯形![]() 的面積為
的面積為![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,故B錯誤;
,故B錯誤;
對于選項C,因為![]() 底面
底面![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() 為直角三角形,
為直角三角形,
又![]() ,所以
,所以![]() ,則
,則![]() 為直角三角形,
為直角三角形,
所以![]() ,
,![]() ,
,
則![]() ,所以
,所以![]() 是直角三角形,
是直角三角形,
故三棱錐![]() 的四個面都是直角三角形,故C錯誤;
的四個面都是直角三角形,故C錯誤;
對于選項D,因為![]() 底面
底面![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,
,
在直角梯形![]() 中,
中,![]() ,
,
所以![]() ,則
,則![]() ,
,
因為![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,故D正確,
,故D正確,
故選:AD


科目:高中數學 來源: 題型:
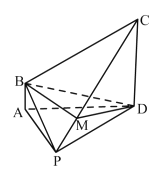
【題目】如圖,在四棱錐PABCD-中,AB//CD,AB=1,CD=3,AP=2,DP=2![]() ,PAD=60°,AB⊥平面PAD,點M在棱PC上.
,PAD=60°,AB⊥平面PAD,點M在棱PC上.
(Ⅰ)求證:平面PAB⊥平面PCD;
(Ⅱ)若直線PA// 平面MBD,求此時直線BP與平面MBD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某旅游區擬建一主題游樂園,該游樂區為五邊形區域ABCDE,其中三角形區域ABE為主題游樂區,四邊形區域為BCDE為休閑游樂區,AB、BC,CD,DE,EA,BE為游樂園的主要道路(不考慮寬度).![]()
![]() .
.

(I)求道路BE的長度;
(Ⅱ)求道路AB,AE長度之和的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E的一個頂點為![]() ,焦點在x軸上,若橢圓的右焦點到直線
,焦點在x軸上,若橢圓的右焦點到直線![]() 的距離是3.
的距離是3.
![]() 求橢圓E的方程;
求橢圓E的方程;
![]() 設過點A的直線l與該橢圓交于另一點B,當弦AB的長度最大時,求直線l的方程.
設過點A的直線l與該橢圓交于另一點B,當弦AB的長度最大時,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面ABCD,底面ABCD為梯形,
底面ABCD,底面ABCD為梯形,![]() ,
,![]() ,且
,且![]() .
.

(1)在PD上是否存在一點F,使得![]() 平面PAB,若存在,找出F的位置,若不存在,請說明理由;
平面PAB,若存在,找出F的位置,若不存在,請說明理由;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
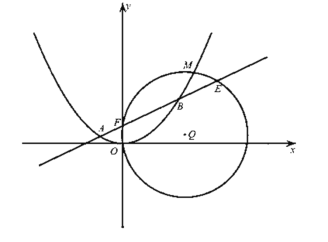
【題目】已知![]() 是拋物線
是拋物線![]() 的焦點,
的焦點,![]() 是拋物線
是拋物線![]() 上一點過
上一點過![]() 三點的圓的圓心為
三點的圓的圓心為![]() ,點
,點![]() 到拋物線
到拋物線![]() 的準線的距離為
的準線的距離為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若點![]() 的橫坐標為4,過
的橫坐標為4,過![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 有兩個不同的交點
有兩個不同的交點![]() ,直線
,直線![]() 與圓
與圓![]() 交于點
交于點![]() ,且點
,且點![]() 的橫坐標大于4,求當
的橫坐標大于4,求當![]() 取得最小值時直線
取得最小值時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com