
【題目】從某企業生產的產品中抽取1000件測量這些產品的一項質量指標值,由測量結果得到頻率分布直方圖如圖所示.
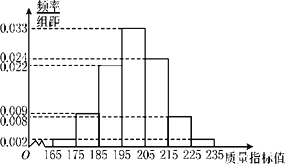
(Ⅰ)求這1000件產品質量指標值的樣本平均數![]() 和樣本方差s2(同一組數據用該區間的中點值作代表).
和樣本方差s2(同一組數據用該區間的中點值作代表).
(Ⅱ)由頻率分布直方圖可以認為這種產品的質量指標值Z服從正態分布N(μ,δ2),其中μ近似為樣本平均數![]() ,δ2近似為樣本方差s2.
,δ2近似為樣本方差s2.
![]() 利用該正態分布,求P(175.6<Z<224.4);
利用該正態分布,求P(175.6<Z<224.4);
②某用戶從該企業購買了100件這種產品,估計其中質量指標值位于區間(175.6,224.4)的產品件數.(精確到個位)
附: ![]() ≈12.2,若Z~N(μ,δ2),則P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),則P(μ-δ<Z<μ+δ)=0.6826,
P(μ-2δ<Z<μ+2δ)=0.9544
【答案】(Ⅰ)![]() ;(Ⅱ)①0.9544,②95件.
;(Ⅱ)①0.9544,②95件.
【解析】試題分析:(Ⅰ)運用離散型隨機變量的期望和方差公式,即可求出;
(Ⅱ)①由(1)知![]() ,從而求出
,從而求出![]() ,即可得出結論;
,即可得出結論;
②由①知,一件產品的質量指標值位于區間(175.6,224.4)的概率為0.9544即可估算..
試題解析:
(Ⅰ)
![]() =170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(Ⅱ)①由(Ⅰ)知,Z~N(200,150),從而
P(175.6<Z<224.4)=P(200-2×12.2<Z<200+2×12.2)=0.9544.
②由①知,一件產品的質量指標值位于區間(175.6,224.4)的概率為0.9544, 用戶從該企業購買了100件這種產品中質量指標值位于區間(175.6,224.4)的產品件數為100×0.9544 ![]() 95 (件)
95 (件)


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左焦點為
的左焦點為![]() ,其左、右頂點為
,其左、右頂點為![]() 、
、![]() ,橢圓與
,橢圓與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,
,![]() 的外接圓的圓心
的外接圓的圓心![]() 在直線
在直線![]() 上.
上.
(I)求橢圓![]() 的方程;
的方程;
(II)已知直線![]() :
:![]() ,
,![]() 是橢圓
是橢圓![]() 上的動點,
上的動點,![]() ,垂足為
,垂足為![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 為等腰三角形?若存在,求出點
為等腰三角形?若存在,求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費用支出![]() 與銷售額
與銷售額![]() 之間有如下的對應數據:
之間有如下的對應數據:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)畫出散點圖;并說明銷售額y與廣告費用支出x之間是正相關還是負相關?
(2)請根據上表提供的數據,求回歸直線方程![]() ;
;
(3)據此估計廣告費用為10時,銷售收入![]() 的值.
的值.
(參考公式: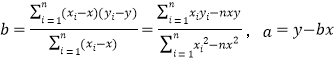 ,).
,).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)為定義在R上的奇函數.如圖是函數圖象的一部分,當0≤x≤2時,是線段OA;當x>2時,圖象是頂點為P(3,4)的拋物線的一部分.
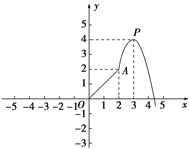
(1)在圖中的直角坐標系中畫出函數f(x)的圖象;
(2)求函數f(x)在[2,+∞)上的解析式;
(3)寫出函數f(x)的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現在頸椎病患者越來越多,甚至大學生也出現了頸椎病,年輕人患頸椎病多與工作、生活方式有關,某調查機構為了了解大學生患有頸椎病是否與長期過度使用電子產品有關,在遂寧市中心醫院隨機的對入院的50名大學生進行了問卷調查,得到了如下的4×4列聯表:
未過度使用 | 過度使用 | 合計 | |
未患頸椎病 | 15 | 5 | 20 |
患頸椎病 | 10 | 20 | 30 |
合計 | 25 | 25 | 50 |
(1)是否有99.5%的把握認為大學生患頸錐病與長期過度使用電子產品有關?
(2)已知在患有頸錐病的10名未過度使用電子產品的大學生中,有3名大學生又患有腸胃炎,現在從上述的10名大學生中,抽取3名大學生進行其他方面的排查,記選出患腸胃炎的學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
參考數據與公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區間
在區間![]() 上為單調遞增函數,求
上為單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的導函數.若正常數
的導函數.若正常數![]() 滿足條件
滿足條件![]() .試比較
.試比較![]() 與0的關系,并給出理由.
與0的關系,并給出理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況.在一般情況下,大橋上的車流速度![]() (單位:千米/小時)是車流密度x(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當
(單位:千米/小時)是車流密度x(單位:輛/千米)的函數.當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當![]() 時,車流速度
時,車流速度![]() 是車流密度x的一次函數.
是車流密度x的一次函數.
①當![]() 時,求函數
時,求函數![]() 的表達式.
的表達式.
②當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)![]() 可以達到最大,并求出最大值(精確到1輛/小時).
可以達到最大,并求出最大值(精確到1輛/小時).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com