
【題目】函數(shù) ![]() 的部分圖像如圖所示,將
的部分圖像如圖所示,將 ![]() 的圖象向右平移
的圖象向右平移 ![]() 個單位長度后得到函數(shù)
個單位長度后得到函數(shù) ![]() 的圖象.
的圖象.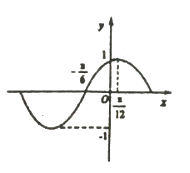
(1)求函數(shù) ![]() 的解折式;
的解折式;
(2)在 ![]() 中,角
中,角 ![]() 滿足
滿足 ![]() ,且其外接圓的半徑
,且其外接圓的半徑 ![]() ,求
,求 ![]() 的面積的最大值.
的面積的最大值.
【答案】
(1)解:由圖知 ![]() ,解得
,解得 ![]()
∵ ![]()
∴ ![]() ,即
,即 ![]()
由于 ![]() ,因此
,因此 ![]()
∴ ![]()
∴ ![]()
![]()
即函數(shù) ![]() 的解析式為
的解析式為 ![]()
(2)解:∵ ![]()
∴ ![]()
∵ ![]() ,
, ![]()
∴ ![]() ,即
,即 ![]() ,
,
∴ ![]() 或1(舍),
或1(舍), ![]()
由正弦定理得 ![]() ,解得
,解得 ![]()
由余弦定理得 ![]()
∴ ![]() ,
, ![]() (當(dāng)且僅當(dāng)
(當(dāng)且僅當(dāng) ![]() 等號成立)
等號成立)
∴ ![]()
∴ ![]() 的面積最大值為
的面積最大值為 ![]()
【解析】(1)根據(jù)圖象知周期T,由周期公式求出ω = 2,由![]() ,結(jié)合φ范圍,得出φ的值,進(jìn)而利用三角函數(shù)圖象的變換規(guī)律即可得解,(2)利用三角函數(shù)恒等變換的應(yīng)用及三角形內(nèi)角和定理化簡可得cosC的值,進(jìn)而得到C的角度,由正弦定理解得c,由余弦定理,基本不等式可求ab≤4,利用面積公式可得面積的最大值.
,結(jié)合φ范圍,得出φ的值,進(jìn)而利用三角函數(shù)圖象的變換規(guī)律即可得解,(2)利用三角函數(shù)恒等變換的應(yīng)用及三角形內(nèi)角和定理化簡可得cosC的值,進(jìn)而得到C的角度,由正弦定理解得c,由余弦定理,基本不等式可求ab≤4,利用面積公式可得面積的最大值.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知矩形 ![]() 所在平面與等腰直角三角形
所在平面與等腰直角三角形 ![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
, ![]() ,
, ![]() 為線段
為線段 ![]() 的中點.
的中點.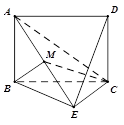
(Ⅰ)證明: ![]() ;
;
(Ⅱ)求 ![]() 與平面
與平面 ![]() 所成的角的余弦值.
所成的角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)國家環(huán)保部新修訂的《環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)》規(guī)定:居民區(qū) ![]() 的年平均濃度不得超過3S微克/立方米,
的年平均濃度不得超過3S微克/立方米, ![]() 的24小時平均濃度不得超過75微克/立方米.某市環(huán)保局隨機(jī)抽取了一居民區(qū)2016年20天
的24小時平均濃度不得超過75微克/立方米.某市環(huán)保局隨機(jī)抽取了一居民區(qū)2016年20天 ![]() 的24小時平均濃度(單位:微克/立方米)的監(jiān)測數(shù)據(jù),數(shù)據(jù)統(tǒng)計如圖表:
的24小時平均濃度(單位:微克/立方米)的監(jiān)測數(shù)據(jù),數(shù)據(jù)統(tǒng)計如圖表:
組別 |
| 頻數(shù)(天) | 頻率 |
第一組 |
| 3 | 0.15 |
第二組 |
| 12 | 0.6 |
第三組 |
| 3 | 0.15 |
第四組 |
| 2 | 0.1 |
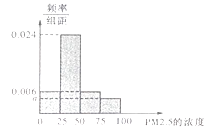
(Ⅰ)將這20天的測量結(jié)果按表中分組方法繪制成的樣本頻率分布直方圖如圖.
(ⅰ)求圖中 ![]() 的值;
的值;
(ⅱ)在頻率分布直方圖中估算樣本平均數(shù),并根據(jù)樣本估計總體的思想,從 ![]() 的年平均濃度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說明理由.
的年平均濃度考慮,判斷該居民區(qū)的環(huán)境質(zhì)量是否需要改善?并說明理由.
(Ⅱ)將頻率視為概率,對于2016年的某3天,記這3天中該居民區(qū) ![]() 的24小時平均濃度符合環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)的天數(shù)為
的24小時平均濃度符合環(huán)境空氣質(zhì)量標(biāo)準(zhǔn)的天數(shù)為 ![]() ,求
,求 ![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() (
( ![]() )在同一半周期內(nèi)的圖象過點
)在同一半周期內(nèi)的圖象過點 ![]() ,
, ![]() ,
, ![]() ,其中
,其中 ![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() 為函數(shù)
為函數(shù) ![]() 圖象的最高點,
圖象的最高點, ![]() 為函數(shù)
為函數(shù) ![]() 的圖象與
的圖象與 ![]() 軸的正半軸的交點,
軸的正半軸的交點, ![]() 為等腰直角三角形.
為等腰直角三角形.
(1)求 ![]() 的值;
的值;
(2)將 ![]() 繞原點
繞原點 ![]() 按逆時針方向旋轉(zhuǎn)角
按逆時針方向旋轉(zhuǎn)角 ![]() ,得到
,得到 ![]() ,若點
,若點 ![]() 恰好落在曲線
恰好落在曲線 ![]() (
( ![]() )上(如圖所示),試判斷點
)上(如圖所示),試判斷點 ![]() 是否也落在曲線
是否也落在曲線 ![]() (
( ![]() )上,并說明理由.
)上,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形 ![]() 中,點
中,點 ![]() 在線段
在線段 ![]() 上,
上, ![]() ,
, ![]() ,沿直線
,沿直線 ![]() 將
將 ![]() 翻折成
翻折成 ![]() ,使點
,使點 ![]() 在平面
在平面 ![]() 上的射影
上的射影 ![]() 落在直線
落在直線 ![]() 上.
上.
(Ⅰ)求證:直線 ![]() 平面
平面 ![]() ;
;
(Ⅱ)求二面角 ![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系 ![]() 中,直線
中,直線 ![]() 過
過 ![]() ,傾斜角為
,傾斜角為 ![]() .以
.以 ![]() 為極點,
為極點, ![]() 軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線
軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線 ![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ![]() .
.
(Ⅰ)求直線 ![]() 的參數(shù)方程和曲線
的參數(shù)方程和曲線 ![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)已知直線 ![]() 與曲線
與曲線 ![]() 交于
交于 ![]() 、
、 ![]() 兩點,且
兩點,且 ![]() ,求直線
,求直線 ![]() 的斜率
的斜率 ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖四邊形 ![]() 中,
中, ![]() 為的
為的 ![]() 內(nèi)角
內(nèi)角 ![]() 的對邊,且滿足
的對邊,且滿足 ![]() .
.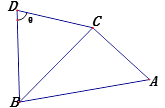
(Ⅰ)證明: ![]() 成等差數(shù)列;
成等差數(shù)列;
(Ⅱ)已知 ![]()
![]() 求四邊形
求四邊形 ![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若執(zhí)行如圖的程序框圖,輸出S的值為4,則判斷框中應(yīng)填入的條件是( )
A.k<14?
B.k<15?
C.k<16?
D.k<17?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() 在圓
在圓![]() :
: ![]() 上,而
上,而![]() 為
為![]() 在
在![]() 軸上的投影,且點
軸上的投影,且點![]() 滿足
滿足![]() ,設(shè)動點
,設(shè)動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若![]() 是曲線
是曲線![]() 上兩點,且
上兩點,且![]() ,
, ![]() 為坐標(biāo)原點,求
為坐標(biāo)原點,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com