
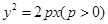 的焦點,與拋物線交于兩點A、B, 將直線
的焦點,與拋物線交于兩點A、B, 將直線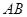 按向量
按向量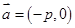 平移得到直線
平移得到直線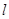 ,
,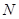 為
為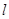 上的動點,
上的動點,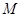 為拋物線弧
為拋物線弧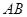 上的動點.
上的動點.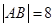 ,求拋物線方程.
,求拋物線方程. 的最大值.
的最大值.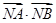 的最小值.
的最小值.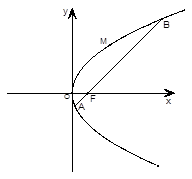
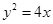 . (2)
. (2) 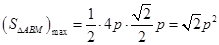 .
. 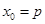 時,
時,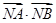 的最小值為
的最小值為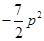 .
.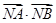
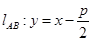 ,則
,則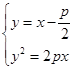 ,消去
,消去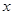 得:
得: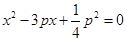 ①,則
①,則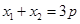 ,由拋物線定義
,由拋物線定義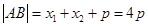 ,
, 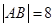 ,即
,即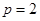 ,則拋物線方程為
,則拋物線方程為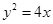 .-------------3分
.-------------3分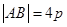 和
和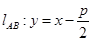 ,設
,設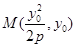 ,則
,則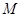 到
到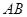 距離:
距離: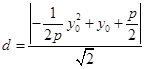 ,因
,因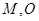 在直線
在直線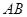 的同側,所以
的同側,所以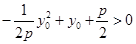 ,
,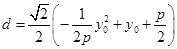 ,即
,即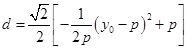 ,
,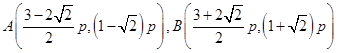
 ,則當
,則當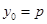 時,
時, 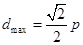 ,
,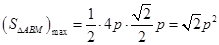 .----------------------8分
.----------------------8分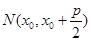 ,
, ,
,
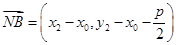 ,
,
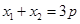 ,
, ,
,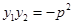 ,
,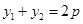 ,則
,則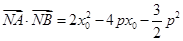 ,即
,即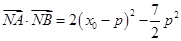 ,當
,當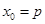 時,
時,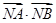 的最小值為
的最小值為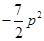 .
.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com