
【題目】已知函數(shù)![]() ,
,
(Ⅰ)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)當(dāng)![]() 時,若
時,若![]() 在區(qū)間
在區(qū)間![]() 上的最小值為-2,其中
上的最小值為-2,其中![]() 是自然對數(shù)的底數(shù),求實數(shù)
是自然對數(shù)的底數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)求出![]() ,由
,由 ![]() 的值可得切點坐標(biāo),由
的值可得切點坐標(biāo),由![]() 的值,可得切線斜率,利用點斜式可得曲線
的值,可得切線斜率,利用點斜式可得曲線![]() 在點
在點![]() 處的切線方程;(2)分三種情況討論
處的切線方程;(2)分三種情況討論![]() 的范圍,在定義域內(nèi),分別令
的范圍,在定義域內(nèi),分別令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間,![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間,根據(jù)單調(diào)性求得函數(shù)最小值,令所求最小值等于
的減區(qū)間,根據(jù)單調(diào)性求得函數(shù)最小值,令所求最小值等于![]() ,排除不合題意的
,排除不合題意的![]() 的取值,即可求得到符合題意實數(shù)
的取值,即可求得到符合題意實數(shù)![]() 的取值范圍.
的取值范圍.
(Ⅰ)當(dāng)![]() 時,
時,![]() ,
,
![]() 因為
因為![]() ,
,
所以切線方程是![]() ;
;
(Ⅱ)函數(shù)![]() 的定義域是
的定義域是![]()
當(dāng)![]() 時,
時,![]()
![]()
令![]() 得
得![]() 或
或![]()
當(dāng)![]() 時,所以
時,所以![]() 在
在![]() 上的最小值是
上的最小值是![]() ,
,
滿足條件,于是![]()
②當(dāng)![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上的最小
上的最小![]() ,
,
即![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增
上單調(diào)遞增
最小值![]() ,不合題意;
,不合題意;
③當(dāng)![]() ,即
,即![]() 時,
時,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
所以![]() 在
在![]() 上的最小值是
上的最小值是![]() ,不合題意.
,不合題意.
綜上所述有,![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線方程為![]() .
.
(1)證明:直線恒過定點;
(2)![]() 為何值時,點
為何值時,點![]() 到直線的距離最大,最大值為多少?
到直線的距離最大,最大值為多少?
(3)若直線分別與![]() 軸,
軸,![]() 軸的負(fù)半軸交于
軸的負(fù)半軸交于![]() 兩點,求
兩點,求![]() 面積的最小值及此時直線的方程.
面積的最小值及此時直線的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)集合![]() ,
, ![]() 是集合
是集合![]() 的所有子集組成的集合.若集合
的所有子集組成的集合.若集合![]() 滿足對任意的映射
滿足對任意的映射![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立,其中,
成立,其中,![]() 表示集合
表示集合![]() 的子集
的子集![]() 的補(bǔ)集,
的補(bǔ)集,![]() 為給定的正整數(shù).試求所有滿足上述條件的集合
為給定的正整數(shù).試求所有滿足上述條件的集合![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 圖象經(jīng)過的定點坐標(biāo);
圖象經(jīng)過的定點坐標(biāo);
(2)當(dāng)![]() 時,求曲線
時,求曲線![]() 在點
在點![]() 處的切線方程及函數(shù)
處的切線方程及函數(shù)![]() 單調(diào)區(qū)間;
單調(diào)區(qū)間;
(3)若對任意![]() ,
,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某兒童樂園在“六一”兒童節(jié)推出了一項趣味活動.參加活動的兒童需轉(zhuǎn)動如圖所示的轉(zhuǎn)盤兩次,每次轉(zhuǎn)動后,待轉(zhuǎn)盤停止轉(zhuǎn)動時,記錄指針?biāo)竻^(qū)域中的數(shù).設(shè)兩次記錄的數(shù)分別為x,y.獎勵規(guī)則如下:
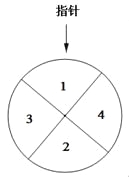
①若![]() ,則獎勵玩具一個;
,則獎勵玩具一個;
②若![]() ,則獎勵水杯一個;
,則獎勵水杯一個;
③其余情況獎勵飲料一瓶.
假設(shè)轉(zhuǎn)盤質(zhì)地均勻,四個區(qū)域劃分均勻.小亮準(zhǔn)備參加此項活動.
(Ⅰ)求小亮獲得玩具的概率;
(Ⅱ)請比較小亮獲得水杯與獲得飲料的概率的大小,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】[選修4-4:坐標(biāo)系與參數(shù)方程]
在極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,以極點為原點
,以極點為原點![]() ,極軸為
,極軸為![]() 軸正半軸(兩坐標(biāo)系取相同的單位長度)的直角坐標(biāo)系
軸正半軸(兩坐標(biāo)系取相同的單位長度)的直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為:
的參數(shù)方程為: ![]() (
(![]() 為參數(shù)).
為參數(shù)).
(1)求曲線![]() 的直角坐標(biāo)方程與曲線
的直角坐標(biāo)方程與曲線![]() 的普通方程;
的普通方程;
(2)將曲線![]() 經(jīng)過伸縮變換
經(jīng)過伸縮變換 后得到曲線
后得到曲線![]() ,若
,若![]() ,
, ![]() 分別是曲線
分別是曲線![]() 和曲線
和曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某群體的人均通勤時間,是指單日內(nèi)該群體中成員從居住地到工作地的平均用時.某地上班族![]() 中的成員僅以自駕或公交方式通勤.分析顯示:當(dāng)
中的成員僅以自駕或公交方式通勤.分析顯示:當(dāng)![]() 中
中![]() (
(![]() )的成員自駕時,自駕群體的人均通勤時間為
)的成員自駕時,自駕群體的人均通勤時間為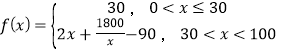 (單位:分鐘),而公交群體的人均通勤時間不受
(單位:分鐘),而公交群體的人均通勤時間不受![]() 影響,恒為
影響,恒為![]() 分鐘,試根據(jù)上述分析結(jié)果回答下列問題:
分鐘,試根據(jù)上述分析結(jié)果回答下列問題:
(1)當(dāng)![]() 在什么范圍內(nèi)時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
在什么范圍內(nèi)時,公交群體的人均通勤時間少于自駕群體的人均通勤時間?
(2)求該地上班族![]() 的人均通勤時間
的人均通勤時間![]() 的表達(dá)式;討論
的表達(dá)式;討論![]() 的單調(diào)性,并說明其實際意義.
的單調(diào)性,并說明其實際意義.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】首屆中國國際進(jìn)口博覽會于2018年11月5日至10日在上海的國家會展中心舉辦.國家展、企業(yè)展、經(jīng)貿(mào)論壇、高新產(chǎn)品匯集……首屆進(jìn)博會高點紛呈.一個更加開放和自信的中國,正用實際行動為世界構(gòu)筑共同發(fā)展平臺,展現(xiàn)推動全球貿(mào)易與合作的中國方案.
某跨國公司帶來了高端智能家居產(chǎn)品參展,供購商洽談采購,并決定大量投放中國市場.已知該產(chǎn)品年固定研發(fā)成本30萬美元,每生產(chǎn)一臺需另投入90美元.設(shè)該公司一年內(nèi)生產(chǎn)該產(chǎn)品![]() 萬臺且全部售完,每萬臺的銷售收入為
萬臺且全部售完,每萬臺的銷售收入為![]() 萬美元,
萬美元,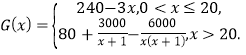
(1)寫出年利潤![]() (萬美元)關(guān)于年產(chǎn)量
(萬美元)關(guān)于年產(chǎn)量![]() (萬臺)的函數(shù)解析式;(利潤=銷售收入-成本)
(萬臺)的函數(shù)解析式;(利潤=銷售收入-成本)
(2)當(dāng)年產(chǎn)量為多少萬臺時,該公司獲得的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(2)當(dāng)![]() 時,設(shè)函數(shù)
時,設(shè)函數(shù)![]() .若存在區(qū)間
.若存在區(qū)間![]() ,使得函數(shù)
,使得函數(shù)![]() 在
在![]() 上的值域為
上的值域為![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com