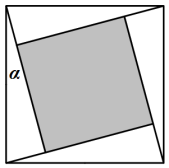
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”，國時期吳國的數學家趙爽創制了一幅“勾股圓方圖”，用數形結合的方法給出了勾股定理的詳細證明
如圖所示的“勾股圓方圖”中，四個相同的直角三角形與中間的小正方形拼成一個大正方形若直角三角形中較小的銳角
，現在向該大止方形區域內隨機地投擲一枚飛鏢，則飛鏢落在陰影部分的概率是
A. 
B. 
C. 
D. 
科目：高中數學 來源： 題型：
【題目】“網購”已經成為我們日常生活中的一部分，某地區隨機調查了100名男性和100名女性在“雙十一”活動中用于網購的消費金額，數據整理如下：
男性消費金額頻數分布表
消費金額 （單位：元） | 0~500 | 500~1000 | 1000~1500 | 1500~2000 | 2000~3000 |
人數 | 15 | 15 | 20 | 30 | 20 |
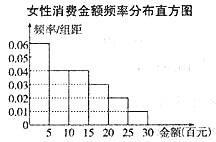
（1）試分別計算男性、女性在此活動中的平均消費金額；
（2）如果分別把男性、女性消費金額與中位數相差不超過200元的消費稱作理性消費，試問是否有5成以上的把握認為理性消費與性別有關.
附：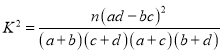
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，
，
，
：
，
：
.給出以下四個命題：
①分別過點
，
，作的不同于
軸的切線，兩切線相交于點
，則點的軌跡為橢圓的一部分；
②若，相切于點
，則點的軌跡恒在定圓上；
③若，相離，且
，則與，都外切的圓的圓心在定橢圓上；
④若，相交，且
，則與，一個內切一個外切的圓的圓心的軌跡為橢圓的一部分.
則以上命題正確的是__________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
過橢圓
的右焦點，且交橢圓于A，B兩點，線段AB的中點是
，
（1）求橢圓的方程；
（2）過原點的直線l與線段AB相交（不含端點）且交橢圓于C，D兩點，求四邊形
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率e滿足
，以坐標原點為圓心，橢圓C的長軸長為半徑的圓與直線
相切.
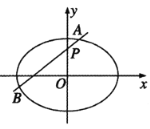
（1）求橢圓C的方程；
（2）過點P(0，1)的動直線
(直線的斜率存在)與橢圓C相交于A，B兩點，問在y軸上是否存在與點P不同的定點Q，使得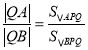
恒成立？若存在，求出定點Q的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在創建“全國衛生文明城”的過程中，環保部門對某市市民進行了一次垃圾分類知識的網絡問卷調查，每一位市民僅有一次參加機會，通過隨機抽樣，得到參加問卷調查的1000人的得分（滿分：100分）數據，統計結果如下表所示.
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
（Ⅰ）已知此次問卷調查的得分
服從正態分布
，
近似為這1000人得分的平均值（同一組中的數據用該組區間的中點值為代表），請利用正態分布的知識求
；
（Ⅱ）在（Ⅰ）的條件下，環保部門為此次參加問卷調查的市民制定如下獎勵方案：
（i）得分不低于的可以獲贈2次隨機話費，得分低于的可以獲贈1次隨機話費；
（ii）每次贈送的隨機話費和相應的概率如下表.現市民甲要參加此次問卷調查，記
為該市民參加問卷調查獲贈的話費，求的分布列及數學期望.
贈送的隨機話費（單位：元） | 20 | 40 |
概率 |
|
|
附：若
，則
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】圖1，在
中，
，
，E為
中點.以
為折痕將
折起，使點C到達點D的位置，且
為直二面角，F是線段
上靠近A的三等分點，連結
，
，
，如圖2.
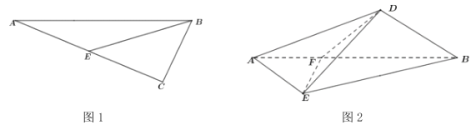
（1）證明：
；
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】波羅尼斯（古希臘數學家，約公元前262-190年）的著作《圓錐曲線論》是古代世界光輝的科學成果，它將圓錐曲線的性質網羅殆盡幾乎使后人沒有插足的余地.他證明過這樣一個命題：平面內與兩定點距離的比為常數k（
且
）的點的軌跡是圓，后人將這個圓稱為阿波羅尼斯圓.現有
，
，則當的面積最大時，AC邊上的高為_______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
