
已知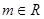 ,對
,對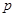 :
: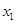 和
和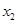 是方程
是方程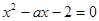 的兩個根,不等式
的兩個根,不等式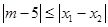 對任意實(shí)數(shù)
對任意實(shí)數(shù)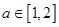 恒成立;
恒成立;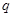 :函數(shù)
:函數(shù)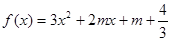 有兩個零點(diǎn),求使“
有兩個零點(diǎn),求使“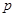 且
且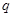 ”為真命題的實(shí)數(shù)的取值范圍。
”為真命題的實(shí)數(shù)的取值范圍。
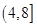
解析試題分析:利用二次方程的韋達(dá)定理求出|x1-x2|,將不等式恒成立轉(zhuǎn)化為求函數(shù)的最值,求出命題p為真命題時m的范圍;利用二次方程有兩個不等根判別式大于0,求出命題Q為真命題時m的范圍;P且Q為真轉(zhuǎn)化為兩個命題全真,求出m的范圍.解:由題設(shè)x1+x2=a,x1x2=-2,∴|x1-x2|=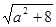 .當(dāng)a∈[1,2]時,
.當(dāng)a∈[1,2]時,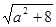 的最小值為3.要使|m-5|≤|x1-x2|對任意實(shí)數(shù)a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+
的最小值為3.要使|m-5|≤|x1-x2|對任意實(shí)數(shù)a∈[1,2]恒成立,只須|m-5|≤3,即2≤m≤8.由已知,得f(x)=3x2+2mx+m+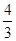 =0的判別式△=4m2-12(m+
=0的判別式△=4m2-12(m+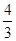 )=4m2-12m-16>0,得m<-1或m>4.綜上,要使“p且q”為真命題,只需P真Q真,即2≤m≤8,m<-1或m>4,解得實(shí)數(shù)m的取值范圍是(4,8].
)=4m2-12m-16>0,得m<-1或m>4.綜上,要使“p且q”為真命題,只需P真Q真,即2≤m≤8,m<-1或m>4,解得實(shí)數(shù)m的取值范圍是(4,8].
考點(diǎn):二次方程的韋達(dá)定理
點(diǎn)評:本題考查二次方程的韋達(dá)定理、二次方程有根的判斷、復(fù)合命題的真假與構(gòu)成其簡單命題的真假的關(guān)系.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知命題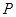 :復(fù)數(shù)
:復(fù)數(shù)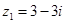 ,復(fù)數(shù)
,復(fù)數(shù)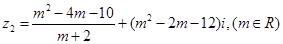 ,
, 是虛數(shù);命題
是虛數(shù);命題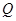 :關(guān)于
:關(guān)于 的方程
的方程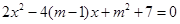 的兩根之差的絕對值小于
的兩根之差的絕對值小于 ;若
;若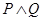 為真命題,求實(shí)數(shù)
為真命題,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
命題p:函數(shù)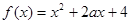 有零點(diǎn);
有零點(diǎn);
命題q:函數(shù)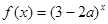 是增函數(shù),
是增函數(shù),
若命題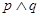 是真命題,求實(shí)數(shù)
是真命題,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知命題 :不等式
:不等式 的解集為R,命題
的解集為R,命題 :
: 是
是 上的增函數(shù),若
上的增函數(shù),若 或
或 為真命題,
為真命題, 且
且 為假命題,求實(shí)數(shù)
為假命題,求實(shí)數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)p:實(shí)數(shù)x滿足x2-4ax+3a2<0(其中a≠0),q:實(shí)數(shù)x滿足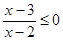
(1)若a=1,且p∧q為真,求實(shí)數(shù)x的取值范圍;
(2)若p是q的必要不充分條件,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
命題p:對任意實(shí)數(shù)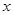 都有
都有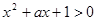 恒成立;命題q :關(guān)于
恒成立;命題q :關(guān)于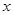 的方程
的方程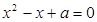 有實(shí)數(shù)根.若“p或q”為真命題,“p且q”為假命題,求實(shí)數(shù)
有實(shí)數(shù)根.若“p或q”為真命題,“p且q”為假命題,求實(shí)數(shù)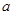 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
命題P:函數(shù)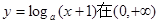 內(nèi)單調(diào)遞減;命題Q:曲線
內(nèi)單調(diào)遞減;命題Q:曲線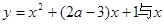 軸交于不同的兩點(diǎn).
軸交于不同的兩點(diǎn).
如果“P\/Q”為真且“P/\Q”為假,求a的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com