
【題目】教育學家分析發現加強語文閱讀理解訓練與提高數學應用題得分率有關,某校興趣小組為了驗證這個結論,從該校選擇甲乙兩個同類班級進行試驗,其中甲班加強閱讀理解訓練,乙班常規教學無額外訓練,一段時間后進行數學應用題測試,統計數據情況如下面的![]() 列聯表(單位:人)
列聯表(單位:人)
優秀人數 | 非優秀人數 | 總計 | |
甲班 |
|
|
|
乙班 |
|
|
|
總計 |
|
|
|
(1)能否據此判斷有![]() 把握認為加強語文閱讀訓練與提高數學應用題得分率有關?
把握認為加強語文閱讀訓練與提高數學應用題得分率有關?
(2)經過多次測試后,小明正確解答一道數學應用題所用的時間在![]() 分鐘,小剛正確解答一道數學應用題所用的時間在
分鐘,小剛正確解答一道數學應用題所用的時間在![]() 分鐘,現小明、小剛同時獨立解答同一道數學應用題,求小剛比小明先正確解答完的概率;
分鐘,現小明、小剛同時獨立解答同一道數學應用題,求小剛比小明先正確解答完的概率;
(3)現從乙班成績優秀的![]() 名同學中任意抽取兩人,并對他們的答題情況進行全程研究,記
名同學中任意抽取兩人,并對他們的答題情況進行全程研究,記![]() 兩人中被抽到的人數為
兩人中被抽到的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
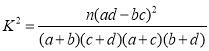
【答案】(1)有![]() 的把握(2)
的把握(2)![]() (3)見解析
(3)見解析
【解析】
試題(1)將數據代人卡方公式計算![]() ,再比較參考數據得把握率(2)所求概率為幾何概率,測度為面積,樣本總體為一個矩形,所求事件為一個三角形,最后根據面積比得概率(3)先確定隨機變量取法,再利用組合數求對應概率,列表得分布列,最后根據期望公式求期望
,再比較參考數據得把握率(2)所求概率為幾何概率,測度為面積,樣本總體為一個矩形,所求事件為一個三角形,最后根據面積比得概率(3)先確定隨機變量取法,再利用組合數求對應概率,列表得分布列,最后根據期望公式求期望
試題解析:解:(1)由表中數據得![]() 的觀測值
的觀測值![]()
所以根據統計有![]() 的把握認為加強語文閱讀理解訓練與提高數學應用題得分率有關.
的把握認為加強語文閱讀理解訓練與提高數學應用題得分率有關.
(2)設小明和小剛解答這道數學應用題的時間分別為![]() 分鐘,
分鐘,
則基本事件滿足的區域為![]() (如圖所示)
(如圖所示) 
設事件![]() 為“小剛比小明先解答完此題” 則滿足的區域為
為“小剛比小明先解答完此題” 則滿足的區域為![]()
![]() 由幾何概型
由幾何概型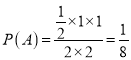 即小剛比小明先解答完此題的概率為
即小剛比小明先解答完此題的概率為![]()
(3)![]() 可能取值為
可能取值為![]() ,
,![]() ,
,![]() ,
,![]()
![]() 的分布列為:
的分布列為:
|
| 1 |
|
|
|
|
|
![]() .
.


 同步奧數系列答案
同步奧數系列答案科目:高中數學 來源: 題型:
【題目】某中學用簡單隨機抽樣方法抽取了100名同學,對其社會實踐次數進行調查,結果如下:
|
|
|
|
|
|
|
男同學人數 | 7 | 15 | 11 | 12 | 2 | 1 |
女同學人數 | 5 | 13 | 20 | 9 | 3 | 2 |
若將社會實踐次數不低于12次的學生稱為“社會實踐標兵”.
(Ⅰ)將頻率視為概率,估計該校1600名學生中“社會實踐標兵”有多少人?
(Ⅱ)從已抽取的8名“社會實踐標兵”中隨機抽取4位同學參加社會實踐表彰活動.
(i)設![]() 為事件“抽取的4位同學中既有男同學又有女同學”,求事件
為事件“抽取的4位同學中既有男同學又有女同學”,求事件![]() 發生的概率;
發生的概率;
(ii)用![]() 表示抽取的“社會實踐標兵”中男生的人數,求隨機變量
表示抽取的“社會實踐標兵”中男生的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() :
:![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,
,![]() 是橢圓上的四個動點,且
是橢圓上的四個動點,且![]() ,
,![]() ,線段
,線段![]() 與
與![]() 交于橢圓
交于橢圓![]() 內一點
內一點![]() .當點
.當點![]() 的坐標為
的坐標為![]() ,且
,且![]() ,
,![]() 分別為橢圓
分別為橢圓![]() 的上頂點和右頂點重合時,四邊形
的上頂點和右頂點重合時,四邊形![]() 的面積為4.
的面積為4.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)證明:當點![]() ,
,![]() ,
,![]() ,
,![]() 在橢圓上運動時,
在橢圓上運動時,![]() (
(![]() )是定值.
)是定值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通指數是交通擁堵指數的簡稱,是綜合反映道路網暢通或擁堵的概念,記交通指數為T.其范圍為[0,10],分別有五個級別:T∈[0,2)暢通;T∈[2,4)基本暢通;T∈[4,6)輕度擁堵;T∈[6,8)中度擁堵;T∈[8,10]嚴重擁堵,晚高峰時段(T≥2),從某市交通指揮中心選取了市區20個交通路段,依據其交通指數數據繪制的部分直方圖如圖所示.
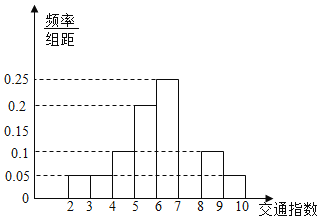
(1)請補全直方圖,并求出輕度擁堵、中度擁堵、嚴重擁堵路段各有多少個?
(2)用分層抽樣的方法從交通指數在[4,6),[6,8),[8,l0]的路段中共抽取6個路段,求依次抽取的三個級別路段的個數;
(3)從(2)中抽出的6個路段中任取2個,求至少一個路段為輕度擁堵的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1的參數方程為![]() (t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2cosθ.
(t為參數).以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2cosθ.
(1)把C1的參數方程化為極坐標方程;
(2)求C1與C2交點的極坐標(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角梯形PBCD中,∠D=∠C![]() ,BC=CD=2,PD=4,A為PD的中點,如圖1,將△PAB沿AB折到△SAB的位置,使SB⊥BC,點E在SD上,如圖2.
,BC=CD=2,PD=4,A為PD的中點,如圖1,將△PAB沿AB折到△SAB的位置,使SB⊥BC,點E在SD上,如圖2.
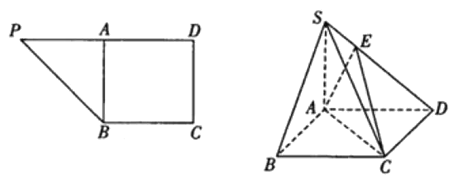
(1)求證:SA⊥平面ABCD;
(2)若E為SD中點,求D點到面EAC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】蝴蝶定理因其美妙的構圖,像是一只翩翩起舞的蝴蝶,一代代數學名家蜂擁而證,正所謂花若芬芳蜂蝶自來.如圖,已知圓![]() 的方程為
的方程為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() .原點
.原點![]() 在圓
在圓![]() 內.
內.

(1)求證:![]() .
.
(2)設![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() .求證:
.求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com