【題目】如圖，是一塊半徑為4米的圓形鐵皮，現打算利用這塊鐵皮做一個圓柱形油桶.具體做法是從
中剪裁出兩塊全等的圓形鐵皮
與
做圓柱的底面，剪裁出一個矩形
做圓柱的側面（接縫忽略不計），
為圓柱的一條母線，點
在上，點
在的一條直徑上，
，
分別與直線
、
相切，都與內切.
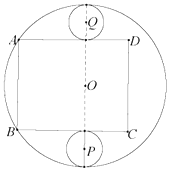
（1）求圓形鐵皮半徑的取值范圍；
（2）請確定圓形鐵皮與半徑的值，使得油桶的體積最大.（不取近似值）
應用題作業本系列答案科目：高中數學 來源： 題型：
【題目】某高校進行自主招生測試，報考學生有500人，其中男生300人，女生200人，為了研究學生的成績是否與性別有關，現采用分層抽樣的方法，從中抽取了100名學生，先統計了他們測試的分數，然后按性別分為男、女兩組，再將兩組學生的分數分成4組：
，
，
，
分別加以統計，得到如圖所示的頻率分布直方圖.
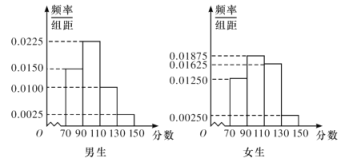
（Ⅰ）根據頻率分布直方圖可以估計女生測試成績的平均值為103.5，請你估計男生測試成績的平均值，由此推斷男、女生測試成績的平均水平的高低；
（Ⅱ）若規定分數不小于110分的學生為“優秀生”，請你根據已知條件完成
列聯表，并判斷是否有
的把握認為“優秀生與性別有關”？
優秀生 | 非優秀生 | 合計 | |
男生 | |||
女生 | |||
合計 |
參考公式：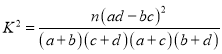
，
.
參考數據：
P（ | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩班舉行數學知識競賽，參賽學生的競賽得分統計結果如下表：
班級 | 參賽人數 | 平均數 | 中位數 | 眾數 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同學分析上表后得到如下結論：
①甲、乙兩班學生的平均成績相同；
②乙班優秀的人數少于甲班優秀的人數（競賽得分
分為優秀）；
③甲、乙兩班成績為85分的學生人數比成績為其他值的學生人數多；
④乙班成績波動比甲班小.
其中正確結論有（ ）
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓柱
底面半徑為1，高為
，
是圓柱的一個軸截面，動點
從點
出發沿著圓柱的側面到達點
，其距離最短時在側面留下的曲線
如圖所示.將軸截面繞著軸逆時針旋轉
后，邊
與曲線相交于點
.
（1）求曲線的長度；
（2）當
時，求點
到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是拋物線
上的兩個點，點
的坐標為
，直線
的斜率為
.設拋物線
的焦點在直線的下方.
（Ⅰ）求k的取值范圍；
（Ⅱ）設C為W上一點，且
，過
兩點分別作W的切線，記兩切線的交點為
. 判斷四邊形
是否為梯形，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為
，其中
為參數，
.在以坐標原點
為極點，軸的正半軸為極軸的極坐標系中，點
的極坐標為
，直線
的極坐標方程為
.
(1)求直線的直角坐標方程與曲線的普通方程；
(2)若
是曲線上的動點，
為線段
的中點.求點到直線的距離的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】定義在
上的偶函數
滿足
，且
，當
時，
.已知方程
在區間
上所有的實數根之和為
.將函數
的圖象向右平移
個單位長度，得到函數
的圖象，則
__________，
__________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）若函數f（x）的圖象在點（2，f（2））處的切線方程為9x﹣y+b＝0，求實數a，b的值；
（2）若a≤0，求f（x）的單調減區間；
（3）對一切實數a∈（0，1），求f（x）的極小值的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人投籃命中的概率分別為
與
，各自相互獨立.現兩人做投籃游戲，共比賽3局，每局每人各投一球.
（1）求比賽結束后甲的進球數比乙的進球數多1的概率；
（2）設
表示比賽結束后甲、乙兩人進球數的差的絕對值，求的概率分布和數學期望
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
