日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
9．袋中裝有紅球3個、白球2個、黑球1個，從中任取2個，則互斥而不對立的兩個事件是（　　）
A．至少有一個白球；至少有一個紅球B．至少有一個白球；紅、黑球各一個
C．恰有一個白球；一個白球一個黑球D．至少有一個白球；都是白球

分析 利用互斥事件、對立事件的定義直接求解．

解答 解：袋中裝有紅球3個、白球2個、黑球1個，從中任取2個，
在A中，至少有一個白球和至少有一個紅球兩個事件能同時發生，不是互斥事件，故A不成立；
在B中，至少有一個白球和紅、黑球各一個兩個事件不能同時發生但能同時不發生，
是互斥而不對立的兩個事件，故B成立；
在C中，恰有一個白球和一個白球一個黑球兩個事件能同時發生，不是互斥事件，故C不成立；
在D中，至少有一個白球和都是白球兩個事件能同時發生，不是互斥事件，故D不成立．
故選：B．

點評 本題考查互斥而不對立事件的判斷，是基礎題，解題時要認真審題，注意互斥事件、對立事件的定義的合理運用．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：解答題

19．已知命題P：函數y=lg（ax2+2x+1）的定義域為R；命題Q：不等式（a-2）x2+2（a-2）x-4＜0對任意實數x恒成立．若P∨Q是真命題，P∧Q是假命題；求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

20．在圓的方程x2+y2+Dx+Ey+F=0中，若D2=E2＞4F，則圓的位置滿足（　　）
A．截兩坐標軸所得弦的長度相等B．與兩坐標軸都相切
C．與兩坐標軸相離D．上述情況都有可能

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

17．已知隨機變量ξ～B（n，p），若$E（ξ）=\frac{5}{3}$，$D（ξ）=\frac{10}{9}$，則n=5，p=$\frac{1}{3}$．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

4．二手車經銷商小王對其所經營的某一型號二手汽車的使用年數x（0＜x≤10）與銷售價格y（單位：萬元/輛）進行整理，得到如下的對應數據：
使用年數246810
售價16139.574.5
（1）若這兩個變量呈線性相關關系，試求y關于x的回歸直線方程$\hat y=\hat bx+\hat a$；
（2）已知小王只收購使用年限不超過10年的二手車，且每輛該型號汽車的收購價格為ω=0.03x2-1.81x+16.2萬元，根據（1）中所求的回歸方程，預測x為何值時，小王銷售一輛該型號汽車所獲得的利潤L（x）最大？
（銷售一輛該型號汽車的利潤=銷售價格-收購價格）
參考公式：$\hat b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

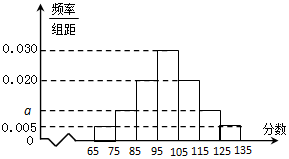14．某校高二年級在一次數學測驗后，隨機抽取了部分學生的數學成績組成一個樣本，得到如下頻率分布直方圖：
（1）求a及這部分學生成績的樣本平均數$\overline x$（同一組數據用該組的中點值作為代表）；
（2）若該校高二共有1000名學生，試估計這次測驗中，成績在105分以上的學生人數．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

1．（1）已知橢圓C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的離心率為$\frac{1}{2}$，以原點為圓心，橢圓的短半軸長為半徑的圓與直線$\sqrt{7}$x-$\sqrt{5}$y+12=0相切．求橢圓C的方程；
（2）已知⊙A1：（x+2）2+y2=12和點A2（2，0），求過點A2且與⊙A1相切的動圓圓心P的軌跡方程．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

18．已知a=cos61°•cos127°+cos29°•cos37°，$b=\frac{{2tan{{13}°}}}{{1+{{tan}^2}{{13}°}}}$，$c=\sqrt{\frac{{1-cos{{50}°}}}{2}}$，則a，b，c的大小關系是（　　）
A．a＜b＜cB．a＞b＞cC．c＞a＞bD．a＜c＜b

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

19．設F1、F2分別是雙曲線C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦點，P是雙曲線C的右支上的點，射線PQ平分∠F1PF2交x軸于點Q，過原點O作PQ的平行線交PF1于點M，若|MP|=$\frac{1}{4}$|F1F2|，則C的離心率為（　　）
A．$\frac{3}{2}$B．3C．2D．$\sqrt{3}$

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 久久精品视频网 | 三级视频网站 | 欧美a级成人淫片免费看 | 日韩三级视频 | 亚洲在线播放 | 久久一级视频 | 另类ts人妖一区二区三区 | 国产在线视频一区 | 色资源在线| 精久久久久 | 欧美做爰xxxⅹ性欧美大片 | 黄色一级免费视频 | 精品国产一区二区三区久久久蜜月 | 日韩欧美在线视频 | 日韩在线免费观看视频 | 久久香蕉网 | 亚洲丝袜视频 | 一区二区免费看 | 国产女人水真多18毛片18精品 | 国产精品国产成人国产三级 | 蜜臀久久99精品久久久久久宅男 | 国产黄色一区二区 | 日韩欧美专区 | 中文字幕一二三四区 | 日韩有码在线视频 | 蜜臀久久99精品久久久久久宅男 | 日韩精品大片 | av超碰在线 | 黄av在线| xxxx亚洲 | 成人激情视频网 | 免费三片在线观看网站v888 | 22精品一区二区三区 | 国产精品高潮呻吟久久 | 精品日韩一区二区三区 | 欧美顶级黄色大片免费 | 中文在线观看免费视频 | 日韩精品三级 | 80日本xxxxxxxxx96| 亚洲成人av在线播放 | 天天草天天干 |