Question

已知二次函數f（x）=ax²+bx+1（a＞0，b∈R），方程f（x）=x有兩個實數根x₁、x₂．
（Ⅰ）如果x₁＜2＜x₂＜4，設函數f（x）的對稱軸為x=x₀，求證x₀＞-1；
（Ⅱ）如果0＜x₁＜2，且f（x）=x的兩實根相差為2，求實數b的取值范圍．

Answer 1

分析：（Ⅰ）有x₁＜2＜x₂＜4轉化為g（x）=f（x）-x=0有兩根：一根在2與4之間，另一根在2的左邊，利用一元二次方程根的分布可證．
（Ⅱ）先有a＞0，知兩根同號，在分兩根均為正和兩根均為負兩種情況來討論．再利用兩根之和與兩根之積和|x₂-x₁|=2來求b的取值范圍．

解答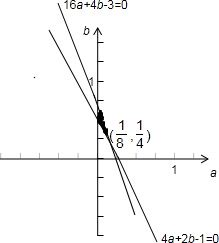：解：（Ⅰ）設g（x）=f（x）-x=ax²+（b-1）x+1，
∵a＞0，
∴由條件x₁＜2＜x₂＜4，
得g（2）＜0，g（4）＞0．即

4a+2b-1＜0 16a+4b-3＞0

由可行域可得

b

a

＜2，∴x0=-

b

2a

＞-1．
（Ⅱ）由題設令g（x）=f（x）-x=ax²+（b-1）x+1=0，知x1x2=

1

a

＞0，故x₁與x₂同號．
0＜x₁＜2，則x₂-x₁=2（負根舍去），
∴x₂=x₁+2＞2．
∴

g(2)＜0 g(4)＞0

，即

4a+2b-1＜0     ① 16a+4b-3＞0    ②

①×4-②得4b-1＜0，∴b＜

1

4

綜上，b的取值范圍為b＜

1

4

．

點評：利用函數的零點求參數范圍問題，通常有兩種解法：一種是利用方程中根與系數的關系或利用函數思想結合圖象求解．二種是構造兩個函數分別作出圖象，利用數形結合求解．此類題目也體現了函數與方程，數形結合的思想