考點:數列與不等式的綜合
專題:計算題,證明題,導數的綜合應用,不等式的解法及應用
分析:(1)求出導數,由極值的定義,得f′(
)=0,得a
n+1=
a
n+2
-n,由b
n=2
n-1•a
n,則b
n+1-b
n=1,由等差數列的通項公式即可得到;
(2)運用錯位相減法求數列的和,注意解題步驟,運用等比數列求和公式即可得到;
(3)運用二項式定理,展開2
n=(1+1)
n,即可得證.
解答:
(1)解:f′(x)=a
nx+2
-n-a
n+1,
由題意得f′(
)=0,得a
n+1=
a
n+2
-n,
由a
n+1=
a
n+2
-n,得2
na
n+1-2
n-1•a
n=1,
由b
n=2
n-1•a
n,則b
n+1-b
n=1,
則數列{b
n}的通項公式b
n=b
1+(n-1)×1=1+n-1=n;
(2)解:由(1)得,a
n=n•2
1-n,
則S
n=1•2
1-1+2×2
1-2+3×2
1-3+…+(n-1)×2
1-(n-1)+n•2
1-n,
2S
n=1×2+2×2
1-1+3×2
1-2+…+n•2
2-n,
兩式相減得,S
n=1×2+1×2
1-1+1×2
1-2+1×2
1-3+…+1×2
1-(n-1)-n•2
1-n=
-n•2
1-n=4-
;
(3)證明:由S
n=4-
=4-
=4-
n>3時,S
n>4-
=4-
=4-
=
.
點評:本題考查導數的運用:求極值,考查數列的通項公式的求法,注意構造數列,運用等差數列的通項公式和等比數列求和公式,考查錯位相減求和,以及二項式定理用于證明不等式的方法,屬于中檔題和易錯題.



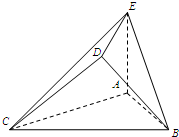 如圖,△ABC是邊長為2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
如圖,△ABC是邊長為2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.