
| A. | $\frac{3}{2}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{2+\sqrt{3}}}{2}$ | D. | $\frac{{4+\sqrt{3}}}{4}$ |
分析 由已知可設$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$,以OA所在直線為x軸建立平面直角坐標系,得到$\overrightarrow{a}、\overrightarrow{b}$的坐標,設出$\overrightarrow{c}$的坐標,利用向量垂直的坐標運算得到C的軌跡,從而求得$\overrightarrow{c\;}•$$\overrightarrow{a\;}$的最大值.
解答 解:由$|{\overrightarrow{b\;}}|=2|{\overrightarrow{a\;}}|=2\overrightarrow{a\;}•\overrightarrow{b\;}=2$,得$|\overrightarrow{a}|=1$,$|\overrightarrow{b}|=2$,$\overrightarrow{a}•\overrightarrow{b}=1$.
設$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b},\overrightarrow{OC}=\overrightarrow{c}$,
以OA所在直線為x軸建立平面直角坐標系,
則$\overrightarrow{a}=(1,0)$,$\overrightarrow{b}=(1,\sqrt{3})$,$\overrightarrow{c}=(x,y)$,$\overrightarrow{c}-\overrightarrow{a}=(x-1,y)$,$\overrightarrow{c}-\overrightarrow{b}=(x-1,y-\sqrt{3})$,
又$({\overrightarrow{c\;}}\right.-$$\left.{\overrightarrow{a\;}})•$$({\overrightarrow{c\;}}\right.-$$\left.{\overrightarrow{b\;}})$=0,
∴$(x-1)^{2}+y(y-\sqrt{3})=0$,即$(x-1)^{2}+(y-\frac{\sqrt{3}}{2})^{2}=\frac{3}{4}$.
又$\overrightarrow{c}•\overrightarrow{a}=x$,∴$\overrightarrow{c\;}•$$\overrightarrow{a\;}$的最大值為1+$\frac{\sqrt{3}}{2}$=$\frac{2+\sqrt{3}}{2}$.
故選:C.
點評 本題考查平面向量的數量積運算,考查數學轉化思想方法,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\sqrt{x-2}$•$\sqrt{x+2}$,y=$\sqrt{{x}^{2}-4}$ | ||
| C. | y=x與y=logaax(a>0且a≠1) | D. | y=|x|,$y={({\sqrt{x}})^2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
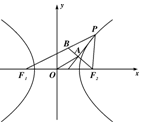 已知F1,F2分別是雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦點,點P在雙曲線上且不與頂點重合,過F2作∠F1PF2的角平分線的垂線,垂足為A.若|OA|=b,則該雙曲線的離心率為( )
已知F1,F2分別是雙曲線$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦點,點P在雙曲線上且不與頂點重合,過F2作∠F1PF2的角平分線的垂線,垂足為A.若|OA|=b,則該雙曲線的離心率為( )| A. | $\frac{{\sqrt{5}+1}}{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}+1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
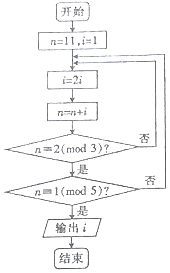 若正整數N除以正整數m后的余數為n,則記為N≡n(bmodm),例如10≡2(bmod4).下面程序框圖的算法源于我國古代聞名中外的《中國剩余定理》.執行該程序框圖,則輸出的i等于( )
若正整數N除以正整數m后的余數為n,則記為N≡n(bmodm),例如10≡2(bmod4).下面程序框圖的算法源于我國古代聞名中外的《中國剩余定理》.執行該程序框圖,則輸出的i等于( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com