
【題目】已知函數 ![]() , (Ⅰ)求函數f(x)的單調區間,并判斷是否有極值;
, (Ⅰ)求函數f(x)的單調區間,并判斷是否有極值;
(Ⅱ)若對任意的x>1,恒有ln(x﹣1)+k+1≤kx成立,求k的取值范圍;
(Ⅲ)證明: ![]() (n∈N+ , n≥2).
(n∈N+ , n≥2).
【答案】解:(Ⅰ) ![]() ,(x>0),
,(x>0), ![]() , 即x∈(0,1),f'(x)>0,當x∈(1,+∞),f'(x)<0,
, 即x∈(0,1),f'(x)>0,當x∈(1,+∞),f'(x)<0,
∴f(x)在區間(0,1)上單調遞增,在區間(1,+∞)上單調遞減,
在x=1處取得極大值,極大值為f(1)=1,無極小值.
(Ⅱ)方法1:∵ln(x﹣1)+k+1≤kx, ![]() ,
,
k≥f(x﹣1)max對任意的x>1恒成立,由(1)知f(x)max=f(1)=1,
則有f(x﹣1)max=1,∴k≥1.
方法2:記g(x)=ln(x﹣1)﹣k(x﹣1)+1,![]() ,
,
當k≤0時,g'(x)≥0;
當k>0時,由g'(x)>0得 ![]() ,
,
即當k≤0時,g(x)在(1,+∞)上為增函數;
當k>0時, ![]() 上為增函數;在
上為增函數;在 ![]() 上為減函數.
上為減函數.
∵對任意的x>1,恒有ln(x﹣1)+k+1≤kx成立,
即要求g(x)≤0恒成立,
∴k>0符合,且 ![]() ,得k≥1.
,得k≥1.
(Ⅲ)證明: ![]() ,由(Ⅰ)知
,由(Ⅰ)知 ![]() ,
,
則 ![]() (當且僅當x=1取等號).
(當且僅當x=1取等號).
令x=n2(n∈N* , n≥2),即 ![]() ,則有
,則有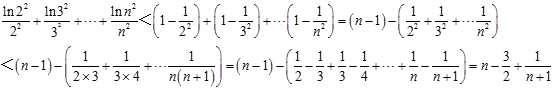
∴ ![]() ,
,
∴ ![]()
【解析】(Ⅰ) ![]() ,(x>0),
,(x>0), ![]() ,分別解出f'(x)>0,f'(x)<0,即可得出單調區間、極值;(Ⅱ)方法1:由ln(x﹣1)+k+1≤kx,分離參數可得:k≥f(x﹣1)max對任意的x>1恒成立,由(I)即可得出. 方法2:記g(x)=ln(x﹣1)﹣k(x﹣1)+1,
,分別解出f'(x)>0,f'(x)<0,即可得出單調區間、極值;(Ⅱ)方法1:由ln(x﹣1)+k+1≤kx,分離參數可得:k≥f(x﹣1)max對任意的x>1恒成立,由(I)即可得出. 方法2:記g(x)=ln(x﹣1)﹣k(x﹣1)+1, ![]() ,對k分類討論研究其單調性即可得出;(Ⅲ)
,對k分類討論研究其單調性即可得出;(Ⅲ) ![]() ,由(Ⅰ)知:
,由(Ⅰ)知: ![]() (當且僅當x=1取等號).令x=n2(n∈N* , n≥2),即
(當且僅當x=1取等號).令x=n2(n∈N* , n≥2),即 ![]() ,再利用“累加求和”、“裂項求和”即可得出.
,再利用“累加求和”、“裂項求和”即可得出.
【考點精析】通過靈活運用利用導數研究函數的單調性和函數的最大(小)值與導數,掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值即可以解答此題.
比較,其中最大的是一個最大值,最小的是最小值即可以解答此題.


 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x),(x∈R)上任一點(x0 , y0)的切線方程為y﹣y0=(x0﹣2)(x02﹣1)(x﹣x0),那么函數f(x)的單調遞減區間是( )
A.[﹣1,+∞)
B.(﹣∞,2]
C.(﹣∞,﹣1)和(1,2)
D.[2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,CAB=90°,AB=AC=2,AA1= ![]() ,M為BC的中點,P為側棱BB1上的動點.
,M為BC的中點,P為側棱BB1上的動點. 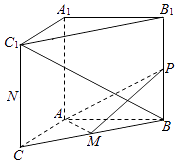
(1)求證:平面APM⊥平面BB1C1C;
(2)試判斷直線BC1與AP是否能夠垂直.若能垂直,求PB的長;若不能垂直,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖正方體ABCD﹣A1B1C1D1 , M,N分別為A1D1和AA1的中點,則下列說法中正確的個數為( ) 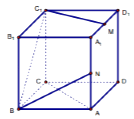
①C1M∥AC;
②BD1⊥AC;
③BC1與AC的所成角為60°;
④B1A1、C1M、BN三條直線交于一點.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩條直線l1:2x+y﹣2=0與l2:2x﹣my+4=0.
(1)若直線l1⊥l2 , 求直線l1與l2交點P的坐標;
(2)若l1 , l2以及x軸圍成三角形的面積為1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一個遞增的等差數列{an}的前三項的和為﹣3,前三項的積為8.數列 ![]() 的前n項和為
的前n項和為 ![]() .
.
(1)求數列{an}的通項公式.
(2)求數列 ![]() 的通項公式.
的通項公式.
(3)是否存在一個等差數列{cn},使得等式 ![]() 對所有的正整數n都成立.若存在,求出所有滿足條件的等差數列{cn}的通項公式,并求數列{bn}的前n項和Tn;若不存在,請說明理由.
對所有的正整數n都成立.若存在,求出所有滿足條件的等差數列{cn}的通項公式,并求數列{bn}的前n項和Tn;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設Ox、Oy是平面內相交成45°角的兩條數軸, ![]() 、
、 ![]() 分別是x軸、y軸正方向同向的單位向量,若向量
分別是x軸、y軸正方向同向的單位向量,若向量 ![]() =x
=x ![]() +y
+y ![]() ,則把有序數對(x,y)叫做向量
,則把有序數對(x,y)叫做向量 ![]() 在坐標系xOy中的坐標,在此坐標系下,假設
在坐標系xOy中的坐標,在此坐標系下,假設 ![]() =(﹣2,2
=(﹣2,2 ![]() ),
), ![]() =(2,0),
=(2,0), ![]() =(5,﹣3
=(5,﹣3 ![]() ),則下列命題不正確的是( )
),則下列命題不正確的是( ) 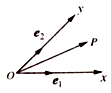
A.![]() =(1,0)
=(1,0)
B.| ![]() |=2
|=2 ![]()
C.![]() ∥
∥ ![]()
D.![]() ⊥
⊥ ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com