
【題目】某市為了制定合理的節電方案,供電局對居民用電情況進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數據按照![]() ,
,![]() 分成9組,制成了如圖所示的頻率直方圖.
分成9組,制成了如圖所示的頻率直方圖.
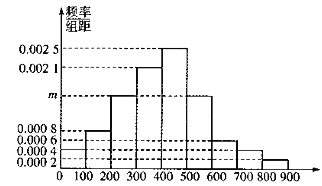
(1)求直方圖中![]() 的值并估計居民月均用電量的中位數;
的值并估計居民月均用電量的中位數;
(2)從樣本里月均用電量不低于700度的用戶中隨機抽取4戶,用![]() 表示月均用電量不低于800度的用戶數,求隨機變量
表示月均用電量不低于800度的用戶數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
【答案】(Ⅰ)![]() ,中位數為408度.(Ⅱ)
,中位數為408度.(Ⅱ)![]() ,分布列見解析.
,分布列見解析.
【解析】試題分析: (Ⅰ)根據頻率分布直方圖中小長方形面積等于對應區間概率,而所有概率和為1,列出方程,解出![]() 的值;因為中位數對應概率為
的值;因為中位數對應概率為![]() ,所以先估計中位數所在區間,再根據概率為
,所以先估計中位數所在區間,再根據概率為![]() ,列方程,解出中位數,(Ⅱ)先根據頻數等于總數與概率的乘積得200戶居民月均用電量在
,列方程,解出中位數,(Ⅱ)先根據頻數等于總數與概率的乘積得200戶居民月均用電量在![]() 度的戶數是8,月均用電量在
度的戶數是8,月均用電量在![]() 度的戶數是4.再確定隨機變量的取法,利用組合數分別計算對應的概率,列表可得分布列,最后根據數學期望公式求期望.
度的戶數是4.再確定隨機變量的取法,利用組合數分別計算對應的概率,列表可得分布列,最后根據數學期望公式求期望.
試題解析:解:(Ⅰ)![]() ,
,
∴![]() .
.
設中位數是![]() 度,前5組的頻率之和為
度,前5組的頻率之和為![]() ,
,
而前4組的頻率之和為![]() ,
,
所以![]() ,
,![]() ,
,
故![]() ,即居民月均用電量的中位數為408度.
,即居民月均用電量的中位數為408度.
(Ⅱ)200戶居民月均用電量在![]() 度的戶數是8,月均用電量在
度的戶數是8,月均用電量在![]() 度的戶數是4.
度的戶數是4.
故隨機變量![]() 的取值為0,1,2,3,4,且
的取值為0,1,2,3,4,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以隨機變量![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
故![]() .
.


科目:高中數學 來源: 題型:
【題目】某工廠36名工人的年齡數據如下表.
工人編號 年齡 | 工人編號 年齡 | 工人編號 年齡 | 工人編號 年齡 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系統抽樣法從36名工人中抽取容量為9的樣本,且在第一分段里用隨機抽樣法抽到的年齡數據為44,列出樣本的年齡數據;
(2)計算(1)中樣本的均值x和方差s2;
(3)36名工人中年齡在![]() 與
與![]() 之間有多少人?所占的百分比是多少(精確到0.01%)?
之間有多少人?所占的百分比是多少(精確到0.01%)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,已知某曲線C的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]()
(1)求該曲線C的直角坐標系方程及離心率![]()
(2)已知點![]() 為曲線C上的動點,求點
為曲線C上的動點,求點![]() 到直線
到直線![]() 的距離的最大值。
的距離的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)=﹣x2+ax﹣2.
(1)若曲線f(x)=xlnx在x=1處的切線與函數g(x)=﹣x2+ax﹣2也相切,求實數a的值;
(2)求函數f(x)在![]() 上的最小值;
上的最小值;
(3)證明:對任意的x∈(0,+∞),都有![]() 成立
成立
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市化工廠三個車間共有工人1 000名,各車間男、女工人數如下表:
第一車間 | 第二車間 | 第三車間 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全廠工人中隨機抽取1名,抽到第二車間男工的可能性是0. 15.
(1)求x的值;
(2)現用分層抽樣的方法在全廠抽取50名工人,問應在第三車間抽取多少名?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 、
、![]() 分別是橢圓
分別是橢圓![]()
![]()
![]() 的左、右焦點,點
的左、右焦點,點![]() 是橢圓
是橢圓![]() 上一點,且
上一點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() ,其中
,其中![]() 為坐標原點,判斷
為坐標原點,判斷![]() 到直線
到直線![]() 的距離是否為定值?若是,求出該定值;若不是,請說明理由.
的距離是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com