
【題目】某工廠36名工人的年齡數據如下表.
工人編號 年齡 | 工人編號 年齡 | 工人編號 年齡 | 工人編號 年齡 |
1 40 | 10 36 | 19 27 | 28 34 |
2 44 | 11 31 | 20 43 | 29 39 |
3 40 | 12 38 | 21 41 | 30 43 |
4 41 | 13 39 | 22 37 | 31 38 |
5 33 | 14 43 | 23 34 | 32 42 |
6 40 | 15 45 | 24 42 | 33 53 |
7 45 | 16 39 | 25 37 | 34 37 |
8 42 | 17 38 | 26 44 | 35 49 |
9 43 | 18 36 | 27 42 | 36 39 |
(1)用系統抽樣法從36名工人中抽取容量為9的樣本,且在第一分段里用隨機抽樣法抽到的年齡數據為44,列出樣本的年齡數據;
(2)計算(1)中樣本的均值x和方差s2;
(3)36名工人中年齡在![]() 與
與![]() 之間有多少人?所占的百分比是多少(精確到0.01%)?
之間有多少人?所占的百分比是多少(精確到0.01%)?
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]()
【解析】試題分析:(1)根據系統抽樣的方法,求出樣本的年齡數據即可;(2)根據平均數和方差的公式求出其平均數和方差即可;(3)求出![]() ﹣s和
﹣s和![]() +s,從而求出其所占的百分比。
+s,從而求出其所占的百分比。
(1)36人分成9組,每組4人,其中第一組的工人年齡為44,所以它在組中的編號為2,所以所有樣本數據的編號為4n-2(n=1,2,…,9),其年齡數據為:44,40,36,43,36,37,44,43,37.
(2)由均值公式知: ![]()
由方差公式知:s2=![]() [(44-40)2+(40-40)2+…+(37-40)2]=
[(44-40)2+(40-40)2+…+(37-40)2]=![]() .
.
(3)因為s2=![]() ,s=
,s=![]() ,所以36名工人中年齡在
,所以36名工人中年齡在![]() -s和
-s和![]() +s之間的人數等于年齡在區間[37,43]上的人數,即40,40,41,…,39,共23人,所以36名工人中年齡在
+s之間的人數等于年齡在區間[37,43]上的人數,即40,40,41,…,39,共23人,所以36名工人中年齡在![]() -s和
-s和![]() +s之間的人數所占的百分比為
+s之間的人數所占的百分比為![]() ×100%≈63.89%.
×100%≈63.89%.


科目:高中數學 來源: 題型:
【題目】甲、乙兩人玩擲骰子游戲,甲擲出的點數記為![]() ,乙擲出的點數記為
,乙擲出的點數記為![]() ,
,
若關于![]() 的一元二次方程
的一元二次方程![]() 有兩個不相等的實數根時甲勝;方程有
有兩個不相等的實數根時甲勝;方程有
兩個相等的實數根時為“和”;方程沒有實數根時乙勝.
(1)列出甲、乙兩人“和”的各種情形;
(2)求甲勝的概率.
必要時可使用此表格
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某出租車公司為了解本公司出租車司機對新法規的知曉情況,隨機對100名出租車司機進行調查,調查問卷共10道題,答題情況如下表所示.
(1)如果出租車司機答對題目數大于等于9,就認為該司機對新法規的知曉情況比較好,試估計該公司的出租車司機對新法規知曉情況比較好的概率;
(2)從答對題目數小于8的出租車司機中任選出2人做進一步的調查,求選出的2人中至少有一名女出租車司機的概率.
答對題目數 | [0,8) | 8 | 9 | 10 |
女 | 2 | 13 | 12 | 8 |
男 | 3 | 37 | 16 | 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:
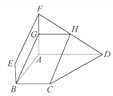
【題目】如圖所示,四邊形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=
90°,BC![]()
![]() AD,BE
AD,BE![]()
![]() FA,G,H分別為FA,FD的中點.
FA,G,H分別為FA,FD的中點.
(1)證明:四邊形BCHG是平行四邊形.
(2)C,D,F,E四點是否共面?為什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在圓![]() 上任取一點
上任取一點![]() ,過點
,過點![]() 作
作![]() 軸的垂線段,
軸的垂線段, ![]() 為垂足,點
為垂足,點![]() 在線段
在線段![]() 上,且
上,且![]() ,點
,點![]() 在圓上運動。
在圓上運動。
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)過定點![]() 的直線與點
的直線與點![]() 的軌跡交于
的軌跡交于![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 為常數,若存在,求出點
為常數,若存在,求出點![]() 的坐標;若不存在,請說明理由。
的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量m=(cosx,-1),n=![]() ,函數f(x)=(m+n)·m.
,函數f(x)=(m+n)·m.
(1)求函數f(x)的最小正周期;
(2)已知a,b,c分別為△ABC內角A,B,C的對邊,A為銳角,a=1,c=![]() ,且f(A)恰是函數f(x)在
,且f(A)恰是函數f(x)在![]() 上的最大值,求A,b和△ABC的面積.
上的最大值,求A,b和△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面給出四種說法:
①用相關指數R2來刻畫回歸效果,R2越小,說明模型的擬合效果越好;
②命題P:“x0∈R,x02﹣x0﹣1>0”的否定是¬P:“x∈R,x2﹣x﹣1≤0”;
③設隨機變量X服從正態分布N(0,1),若P(x>1)=p則P(﹣1<X<0)=![]() ﹣p
﹣p
④回歸直線一定過樣本點的中心(![]() ).
).
其中正確的說法有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了制定合理的節電方案,供電局對居民用電情況進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數據按照![]() ,
,![]() 分成9組,制成了如圖所示的頻率直方圖.
分成9組,制成了如圖所示的頻率直方圖.
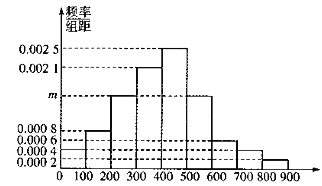
(1)求直方圖中![]() 的值并估計居民月均用電量的中位數;
的值并估計居民月均用電量的中位數;
(2)從樣本里月均用電量不低于700度的用戶中隨機抽取4戶,用![]() 表示月均用電量不低于800度的用戶數,求隨機變量
表示月均用電量不低于800度的用戶數,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com