
設函數 ,
, 是定義域為R上的奇函數.
是定義域為R上的奇函數.
(1)求 的值,并證明當
的值,并證明當 時,函數
時,函數 是R上的增函數;
是R上的增函數;
(2)已知 ,函數
,函數 ,
, ,求
,求 的值域;
的值域;
(3)若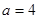 ,試問是否存在正整數
,試問是否存在正整數 ,使得
,使得 對
對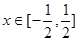 恒成立?若存在,請求出所有的正整數
恒成立?若存在,請求出所有的正整數 ;若不存在,請說明理由.
;若不存在,請說明理由.
(1)如下(2)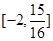 (3)存在正整數
(3)存在正整數 =3或4
=3或4
解析試題分析:解:(1)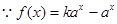 是定義域為R上的奇函數,
是定義域為R上的奇函數,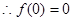 ,得
,得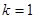 .
.
此時,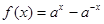 ,
,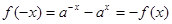 ,即
,即 是R上的奇函數.
是R上的奇函數.
設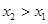 ,則
,則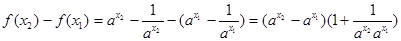 ,
,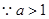 ,
,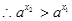 ,
,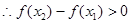 ,
,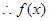 在R上為增函數.
在R上為增函數.
(2)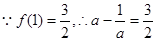 ,即
,即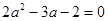 ,
,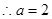 或
或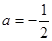 (舍去),
(舍去),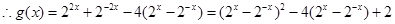
令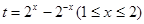 ,由(1)知
,由(1)知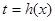 在[1,2]上為增函數,∴
在[1,2]上為增函數,∴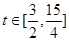 ,
,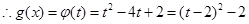 ,
,
當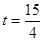 時,
時, 有最大值
有最大值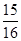 ;當
;當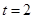 時,
時, 有最小值
有最小值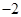 ,
,
∴ 的值域
的值域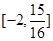 .
.
(3)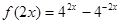 =
=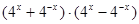 ,
,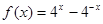 ,
,
假設存在滿足條件的正整數 ,則
,則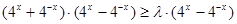 ,
,
①當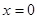 時,
時,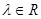 .
.
②當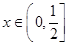 時,
時,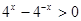 ,則
,則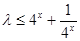 ,令
,令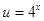 ,則
,則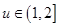 ,易證
,易證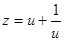 在
在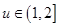 上是增函數,∴
上是增函數,∴ .
.
③當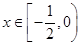 時,
時,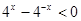 ,則
,則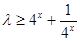 ,令
,令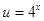 ,則
,則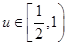 ,易證
,易證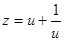 在
在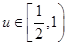 上是減函數,∴
上是減函數,∴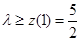 .
.
綜上所述,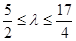 ,∵
,∵ 是正整數,∴
是正整數,∴ =3或4.
=3或4.
∴存在正整數 =3或4,使得
=3或4,使得 對
對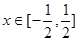 恒成立.
恒成立.
考點:函數的單調性
點評:本題難度較大。函數的單調性對求最值、判斷函數值大小關系和證明不等式都有較大幫助,而求函數的單調性有時可以結合導數來求。


科目:高中數學 來源: 題型:解答題
某造船公司年造船量是20艘,已知造船x艘的產值函數為R(x)=3700x+45x2-10x3(單位:萬元),成本函數為C(x)=460x+5000(單位:萬元),又在經濟學中,函數f(x)的邊際函數Mf(x)定義為Mf(x)=f(x+1)-f(x).
(1)求利潤函數P(x)及邊際利潤函數MP(x);(提示:利潤=產值-成本)
(2)問年造船量安排多少艘時,可使公司造船的年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2013年,首都北京經歷了59年來霧霾天氣最多的一個月。經氣象局統計,北京市從1月1日至1月30日這30天里有26天出現霧霾天氣。《環境空氣質量指數(AQI)技術規定(試行)》將空氣質量指數分為六級:其中,中度污染(四級),指數為151—200;重度污染(五級),指數為201—300;嚴重污染(六級),指數大于300. 下面表1是該觀測點記錄的4天里,AQI指數 與當天的空氣水平可見度
與當天的空氣水平可見度 (千米)的情況,表2是某氣象觀測點記錄的北京1月1日到1月30日AQI指數頻數統計結果,
(千米)的情況,表2是某氣象觀測點記錄的北京1月1日到1月30日AQI指數頻數統計結果,
表1:AQI指數 與當天的空氣水平可見度
與當天的空氣水平可見度 (千米)情況
(千米)情況
AQI指數 |  |  |  |  |
空氣可見度 (千米) (千米) |  |  |  |  |
| AQI指數 |  |  |  |  |  |
| 頻數 | 3 | 6 | 12 | 6 | 3 |
 ,根據表1的數據,求出
,根據表1的數據,求出 關于
關于 的線性回歸方程;
的線性回歸方程;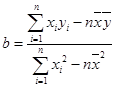 ,
, )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 ,及函數
,及函數 。
。
關于 的不等式
的不等式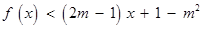 的解集為
的解集為 ,其中
,其中 為正常數。
為正常數。
(1)求 的值;
的值;
(2) R
R 如何取值時,函數
如何取值時,函數

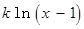 存在極值點,并求出極值點;
存在極值點,并求出極值點;
(3)若 ,且
,且
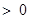 ,求證:
,求證:
 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某公司生產一種產品,每年需投入固定成本0.5萬元,此外每生產1百件這樣的產品,還需增加投入0.25萬元,經市場調查知這種產品年需求量為5百件,產品銷售數量為t(百件)時,銷售所得的收入為( )萬元。
)萬元。
(1)該公司這種產品的年生產量為 百件,生產并銷售這種產品得到的利潤為當年產量
百件,生產并銷售這種產品得到的利潤為當年產量 的函數
的函數 ,求
,求 ;
;
(2)當該公司的年產量為多大時當年所獲得的利潤最大。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某海邊旅游景點有50輛自行車供游客租賃使用,管理這些自行車的費用是每日115元。根據經驗,若每輛自行車的日租金不超過6元,則自行車可以全部租出;若超出6元,則每超過1元,租不出的自行車就增加3輛。為了便于結算,每輛自行車的日租金 (元)只取整數,并且要求出租自行車一日的總收入必須高于這一日的管理費用,用
(元)只取整數,并且要求出租自行車一日的總收入必須高于這一日的管理費用,用 (元)表示出租自行車的日凈收入(即一日中出租自行車的總收入減去管理費用后的所得).
(元)表示出租自行車的日凈收入(即一日中出租自行車的總收入減去管理費用后的所得).
(Ⅰ)求函數 的解析式及其定義域;
的解析式及其定義域;
(Ⅱ)試問當每輛自行車的日租金定為多少元時,才能使一日的凈收入最多?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有一批貨物需要用汽車從生產商所在城市甲運至銷售商所在城市乙.已知從城市甲到城市乙只有兩條公路,且通過這兩條公路所用的時間互不影響.
據調查統計,通過這兩條公路從城市甲到城市乙的200輛汽車所用時間的頻數分布如下表:
| 所用的時間(天數) | 10 | 11 | 12 | 13 |
| 通過公路1的頻數 | 20 | 40 | 20 | 20 |
| 通過公路2的頻數 | 10 | 40 | 40 | 10 |
 萬元、
萬元、 萬元(其它費用忽略不計),此項費用由生產商承擔.如果生產商恰能在約定日期當天將貨物送到,則銷售商一次性支付給生產商40萬元,若在約定日期前送到,每提前一天銷售商將多支付給生產商2萬元;若在約定日期后送到,每遲到一天,銷售商將少支付給生產商2萬元.如果汽車A、B長期按(Ⅰ)所選路徑運輸貨物,試比較哪輛汽車為生產商獲得的毛利潤更大.(注:毛利潤=(銷售商支付給生產商的費用)一(一次性費用)) .
萬元(其它費用忽略不計),此項費用由生產商承擔.如果生產商恰能在約定日期當天將貨物送到,則銷售商一次性支付給生產商40萬元,若在約定日期前送到,每提前一天銷售商將多支付給生產商2萬元;若在約定日期后送到,每遲到一天,銷售商將少支付給生產商2萬元.如果汽車A、B長期按(Ⅰ)所選路徑運輸貨物,試比較哪輛汽車為生產商獲得的毛利潤更大.(注:毛利潤=(銷售商支付給生產商的費用)一(一次性費用)) .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com