
某造船公司年造船量是20艘,已知造船x艘的產值函數為R(x)=3700x+45x2-10x3(單位:萬元),成本函數為C(x)=460x+5000(單位:萬元),又在經濟學中,函數f(x)的邊際函數Mf(x)定義為Mf(x)=f(x+1)-f(x).
(1)求利潤函數P(x)及邊際利潤函數MP(x);(提示:利潤=產值-成本)
(2)問年造船量安排多少艘時,可使公司造船的年利潤最大?
(1)P(x)= -10x3+45x2+3 240x-5 000(x∈N*,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3 275 (x∈N*,且1≤x≤19)
(2)x=12時,P(x)有最大值
解析試題分析:解:(1)P(x)=R(x)-C(x)=-10x3+45x2+3 240x-5 000(x∈N*,且1≤x≤20);
MP(x)=P(x+1)-P(x)=-30x2+60x+3 275 (x∈N*,且1≤x≤19). 4分
(2)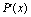 =-30x2+90x+3 240=-30(x-12)(x+9),
=-30x2+90x+3 240=-30(x-12)(x+9),
∵x>0,∴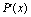 =0時,x=12, 8分
=0時,x=12, 8分
∴當0<x<12時,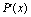 >0,當x>12時,
>0,當x>12時,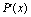 <0,
<0,
∴x=12時,P(x)有最大值. 11分
即年造船量安排12艘時,可使公司造船的年利潤最大. 12分
考點:函數的運用
點評:主要是考查了函數模型的運用,分析問題和解決問題能力的運用,屬于中檔題。


 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案科目:高中數學 來源: 題型:解答題
設函數
 .
.
(1) 試問函數f(x)能否在x=  時取得極值?說明理由;
時取得極值?說明理由;
(2) 若a=  ,當x∈[
,當x∈[ ,4]時,函數f(x)與g(x)的圖像有兩個公共點,求c的取值范圍.
,4]時,函數f(x)與g(x)的圖像有兩個公共點,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
若二次函數f(x)=ax2+bx+c(a≠0)滿足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在區間[-1,1]上,不等式f(x)>2x+m恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠生產一種產品的原材料費為每件40元,若用x表示該廠生產這種產品的總件數,則電力與機器保養等費用為每件0.05x元,又該廠職工工資固定支出12500元。
(1)把每件產品的成本費P(x)(元)表示成產品件數x的函數,并求每件產品的最低成本費;
(2)如果該廠生產的這種產品的數量x不超過3000件,且產品能全部銷售,根據市場調查:每件產品的銷售價Q(x)與產品件數x有如下關系: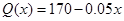 ,試問生產多少件產品,總利潤最高?(總利潤=總銷售額-總的成本)
,試問生產多少件產品,總利潤最高?(總利潤=總銷售額-總的成本)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
將邊長為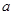 米的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少米?方盒的最大容積為多少?
米的一塊正方形鐵皮的四角各截去一個大小相同的小正方形,然后將四邊折起做成一個無蓋的方盒.欲使所得的方盒有最大容積,截去的小正方形的邊長應為多少米?方盒的最大容積為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 ,
, 是定義域為R上的奇函數.
是定義域為R上的奇函數.
(1)求 的值,并證明當
的值,并證明當 時,函數
時,函數 是R上的增函數;
是R上的增函數;
(2)已知 ,函數
,函數 ,
, ,求
,求 的值域;
的值域;
(3)若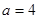 ,試問是否存在正整數
,試問是否存在正整數 ,使得
,使得 對
對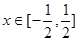 恒成立?若存在,請求出所有的正整數
恒成立?若存在,請求出所有的正整數 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com