
【題目】寒冷的冬天,某高中一組學生來到一大棚蔬菜基地,研究種子發芽與溫度控制技術的關系,他們分別記錄五組平均溫度及種子的發芽數,得到如下數據:
平均溫度 | 11 | 10 | 13 | 9 | 12 |
發芽數 | 25 | 23 | 30 | 16 | 26 |
(Ⅰ)若從五組數據中選取兩組數據,求這兩組數據平均溫度相差不超過![]() 概率;
概率;
(Ⅱ)求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅲ)若由線性回歸方程得到的估計數據與實際數據的誤差不超過2顆,則認為得到的線性回歸方程是可靠的,試問(Ⅱ)屮所得的線性回歸方程是否可靠?
(注:  ,
, ![]() )
)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)見解析.
;(Ⅲ)見解析.
【解析】試題分析:(Ⅰ)利用列舉法可得五組數據中選取兩組數據總事件數為![]() ,兩組數據平均溫度相差不超過
,兩組數據平均溫度相差不超過![]() 的事件數為
的事件數為![]() ,由古典概型概率公式可得結果;(Ⅱ)根據表格中的數據及平均數公式可求出
,由古典概型概率公式可得結果;(Ⅱ)根據表格中的數據及平均數公式可求出![]() 與
與![]() 的值可得樣本中心點的坐標,從而求可得公式
的值可得樣本中心點的坐標,從而求可得公式 中所需數據,求出
中所需數據,求出![]() 的值,再結合樣本中心點的性質可得
的值,再結合樣本中心點的性質可得![]() 的值,進而可得
的值,進而可得![]() 關于
關于![]() 的回歸方程;(Ⅲ)將表格中所給
的回歸方程;(Ⅲ)將表格中所給![]() 的值代入回歸方程求出的
的值代入回歸方程求出的![]() 值與表格中對應
值與表格中對應![]() 值比較即可的結果.
值比較即可的結果.
試題解析:(Ⅰ)設![]() ,則基本事件為
,則基本事件為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所以
,所以![]()
(Ⅱ)![]() ,
, ![]()
![]()
![]()
![]()
![]()

![]()
![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]()
(Ⅲ)利用回歸方程![]() 得到五組估計數據如圖
得到五組估計數據如圖
平均溫度 | 11 | 10 | 13 | 9 | 12 |
發芽數 | 25 | 23 | 30 | 16 | 26 |
估計發芽數 | 24 | 21 | 30 | 18 | 27 |
所以線性回歸方程![]() 是可靠的.
是可靠的.
(注只要驗證一兩個數據且結論正確可給兩分)
【方法點晴】本題主要考查古典概型概率公式以及線性回歸方程的求法與應用,屬于中檔題.求回歸直線方程的步驟:①依據樣本數據畫出散點圖,確定兩個變量具有線性相關關系;②計算![]() 的值;③計算回歸系數
的值;③計算回歸系數![]() ;④寫出回歸直線方程為
;④寫出回歸直線方程為![]() ; 回歸直線過樣本點中心
; 回歸直線過樣本點中心![]() 是一條重要性質,利用線性回歸方程可以估計總體,幫助我們分析兩個變量的變化趨勢.
是一條重要性質,利用線性回歸方程可以估計總體,幫助我們分析兩個變量的變化趨勢.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】某工廠為了對研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
銷量 | 100 | 94 | 93 | 90 | 85 | 78 |
預計在今后的銷售中,銷量與單價仍然服從這種線性相關關系,且該產品的成本是5元/件,為使工廠獲得最大利潤,該產品的單價應定為( )
(附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率的最小二乘估計值為
的斜率的最小二乘估計值為 .參考數值:
.參考數值:![]() ,
,![]() )
)
A. 9.4元 B. 9.5元 C. 9.6元 D. 9.7元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 且x,
且x,![]() .
.
(1)判斷![]() 的奇偶性,并用定義證明;
的奇偶性,并用定義證明;
(2)若不等式![]() 在
在![]() 上恒成立,試求實數a的取值范圍;
上恒成立,試求實數a的取值范圍;
(3)![]() 的值域為
的值域為![]() 函數
函數![]() 在
在![]() 上的最大值為M,最小值為m,若
上的最大值為M,最小值為m,若![]() 成立,求正數a的取值范圍.
成立,求正數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2016·北京卷)如圖,在四棱錐P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
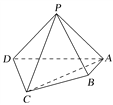
(1)求證:PD⊥平面PAB;
(2)求直線PB與平面PCD所成角的正弦值;
(3)在棱PA上是否存在點M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 經過點
經過點![]() ,且和直線
,且和直線![]() 相切.
相切.
(Ⅰ)求該動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)已知點![]() ,若斜率為1的直線
,若斜率為1的直線![]() 與線段
與線段![]() 相交(不經過坐標原點
相交(不經過坐標原點![]() 和點
和點![]() ),且與曲線
),且與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0),四點P1(1,1),P2(0,1),P3(–1,
(a>b>0),四點P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三點在橢圓C上.
)中恰有三點在橢圓C上.
(1)求C的方程;
(2)設直線l不經過P2點且與C相交于A,B兩點.若直線P2A與直線P2B的斜率的和為–1,證明:l過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過橢圓![]() 的左焦點的直線
的左焦點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,直線
兩點,直線![]() 過坐標原點且與直線
過坐標原點且與直線![]() 的斜率互為相反數.若直線
的斜率互為相反數.若直線![]() 與橢圓交于
與橢圓交于![]() 兩點且均不與點
兩點且均不與點![]() 重合,設直線
重合,設直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,直線
,直線![]() 與
與![]() 軸所成的銳角為
軸所成的銳角為![]() ,判斷
,判斷![]() 與
與![]() 的大小關系并加以證明.
的大小關系并加以證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com