
【題目】從某小區抽取50戶居民進行月用電量調查,發現其用電量都在50到350度之間,將用電量的數據繪制成頻率分布直方圖如下.

(1)求頻率分布直方圖中![]() 的值并估計這50戶用戶的平均用電量;
的值并估計這50戶用戶的平均用電量;
(2)若將用電量在區間![]() 內的用戶記為
內的用戶記為![]() 類用戶,標記為低用電家庭,用電量在區間
類用戶,標記為低用電家庭,用電量在區間![]() 內的用戶記為
內的用戶記為![]() 類用戶,標記為高用電家庭,現對這兩類用戶進行問卷調查,讓其對供電服務進行打分,打分情況見莖葉圖:
類用戶,標記為高用電家庭,現對這兩類用戶進行問卷調查,讓其對供電服務進行打分,打分情況見莖葉圖:
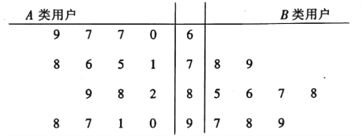
①從![]() 類用戶中任意抽取3戶,求恰好有2戶打分超過85分的概率;
類用戶中任意抽取3戶,求恰好有2戶打分超過85分的概率;
②若打分超過85分視為滿意,沒超過85分視為不滿意,請填寫下面列聯表,并根據列聯表判斷是否有![]() 的把握認為“滿意度與用電量高低有關”?
的把握認為“滿意度與用電量高低有關”?
滿意 | 不滿意 | 合計 | |
| |||
| |||
合計 |
附表及公式:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
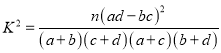 ,
, ![]() .
.
【答案】(1)![]() ,186(2)
,186(2)![]() 沒有
沒有
【解析】試題分析:(1)由矩形面積和為1,求得![]() ,再由每一個矩形的中點橫坐標乘以矩形面積求和可得平均值;
,再由每一個矩形的中點橫坐標乘以矩形面積求和可得平均值;
(2)①![]() 類用戶共9人,打分超過85分的有6人,則
類用戶共9人,打分超過85分的有6人,則![]() 即為所求;
即為所求;
(2)根據數據完成列聯表,利用 ,計算查表下結論即可.
,計算查表下結論即可.
試題解析:
解:(1)![]()
![]() ,
,
按用電量從低到高的六組用戶數分別為6,9,15,11,6,3,
所以估計平均用電量為![]()
![]() 度.
度.
(2)①![]() 類用戶共9人,打分超過85分的有6人,所以從
類用戶共9人,打分超過85分的有6人,所以從![]() 類用戶中任意抽取3戶,恰好有2戶打分超過85分的概率為
類用戶中任意抽取3戶,恰好有2戶打分超過85分的概率為![]() .
.
②
滿意 | 不滿意 | 合計 | |
| 6 | 9 | 15 |
| 6 | 3 | 9 |
合計 | 12 | 12 | 24 |
因為![]() 的觀測值
的觀測值![]()
![]() ,
,
所以沒有![]() 的把握認為“滿意與否與用電量高低有關”.
的把握認為“滿意與否與用電量高低有關”.


科目:高中數學 來源: 題型:
【題目】如圖,游客從景點![]() 下山至
下山至![]() 有兩種路徑:一種是從
有兩種路徑:一種是從![]() 沿直線步行到
沿直線步行到![]() ,另一種是先從
,另一種是先從![]() 乘纜車到
乘纜車到![]() ,然后從
,然后從![]() 沿直線步行到
沿直線步行到![]() .現有甲、乙兩位游客從
.現有甲、乙兩位游客從![]() 下山,甲沿
下山,甲沿![]() 勻速步行,速度為
勻速步行,速度為![]() 米/分鐘.在甲出發
米/分鐘.在甲出發![]() 分鐘后,乙從
分鐘后,乙從![]() 乘纜車到
乘纜車到![]() ,在
,在![]() 處停留
處停留![]() 分鐘后,再從
分鐘后,再從![]() 勻速步行到
勻速步行到![]() .已知纜車從
.已知纜車從![]() 到
到![]() 要
要![]() 分鐘,
分鐘,![]() 長為
長為![]() 米,若
米,若![]() ,
,![]() .為使兩位游客在
.為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() 分鐘,則乙步行的速度
分鐘,則乙步行的速度![]() (米/分鐘)的取值范圍是 __________.
(米/分鐘)的取值范圍是 __________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為提升教師專業功底,引領青年教師成長,某市教育局舉行了全市“園丁杯”課堂教學比賽,在這次比賽中,通過采用錄像課評比的片區預賽,有![]() 共10位選手脫穎而出進入全市決賽.決賽采用現場上課形式,從學科評委庫中采用隨機抽樣抽選代號1,2,3,…,7的7名評委,規則是:選手上完課,評委們當初評分,并從7位評委評分中去掉一個最高分,去掉一個最低分,根據剩余5位評委的評分,算出平均分作為該選手的最終得分.記評委
共10位選手脫穎而出進入全市決賽.決賽采用現場上課形式,從學科評委庫中采用隨機抽樣抽選代號1,2,3,…,7的7名評委,規則是:選手上完課,評委們當初評分,并從7位評委評分中去掉一個最高分,去掉一個最低分,根據剩余5位評委的評分,算出平均分作為該選手的最終得分.記評委![]() 對某選手評分排名與該選手最終排名的差的絕對值為“評委
對某選手評分排名與該選手最終排名的差的絕對值為“評委![]() 對這位選手的分數排名偏差”
對這位選手的分數排名偏差”![]() .排名規則:由高到低依次排名,如果選手分數一樣,認定名次并列(如:選手
.排名規則:由高到低依次排名,如果選手分數一樣,認定名次并列(如:選手![]() 分數一致排在第二,則認為他們同屬第二名,沒有第三名,接下來分數為第四名).七位評委評分情況如下表所示:
分數一致排在第二,則認為他們同屬第二名,沒有第三名,接下來分數為第四名).七位評委評分情況如下表所示:
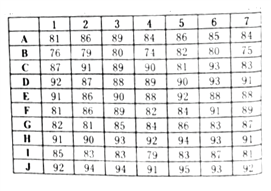
(1)根據最終評分表,填充如下表格:

(2)試借助評委評分分析表,根據評委對各選手的排名偏差的平方和,判斷評委4與評委5在這次活動中誰評判更準確.
____號評委評分分析表
選手 | A | B | C | D | E | F | G | H | I | J |
最終排名 | ||||||||||
評分排名 | ||||||||||
排名偏差 |
(3)從這10位選手中任意選出3位,記其中評委4比評委5對選手排名偏差小的選手數位![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】朱世杰是歷史上最偉大的數學家之一,他所著的![]() 四元玉鑒
四元玉鑒![]() 卷中“如像招數”五問有如下問題:“今有官司差夫一千八百六十四人筑堤
卷中“如像招數”五問有如下問題:“今有官司差夫一千八百六十四人筑堤![]() 只云初日差六十四人,次日轉多七人,每人日支米三升,共支米四百三石九斗二升,問筑堤幾日”
只云初日差六十四人,次日轉多七人,每人日支米三升,共支米四百三石九斗二升,問筑堤幾日”![]() 其大意為:“官府陸續派遣
其大意為:“官府陸續派遣![]() 人前往修筑堤壩,第一天派出
人前往修筑堤壩,第一天派出![]() 人,從第二天開始,每天派出的人數比前一天多
人,從第二天開始,每天派出的人數比前一天多![]() 人,修筑堤壩的每人每天分發大米
人,修筑堤壩的每人每天分發大米![]() 升,共發出大米
升,共發出大米![]() 升,問修筑堤壩多少天”
升,問修筑堤壩多少天”![]() 這個問題中,前
這個問題中,前![]() 天一共應發大米____________升.
天一共應發大米____________升.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函數
.已知函數![]() ,
,![]() .
.
(1)設![]() ,求函數
,求函數![]() 在
在![]() 上零點的個數;
上零點的個數;
(2)試探討是否存在實數![]() ,使得
,使得![]() 對
對![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經觀測,某公路段在某時段內的車流量![]() (千輛/小時)與汽車的平均速度
(千輛/小時)與汽車的平均速度![]() (千米/小時)之間有函數關系:
(千米/小時)之間有函數關系:![]() .
.
(1)在該時段內,當汽車的平均速度![]() 為多少時車流量
為多少時車流量![]() 最大?最大車流量為多少?(精確到0.01)
最大?最大車流量為多少?(精確到0.01)
(2)為保證在該時段內車流量至少為10千輛/小時,則汽車的平均速度應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),曲線
為參數),曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
,![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com