【題目】已知數列
的前
項和為
,且
.
(1)求數列的通項公式；
(2)設數列
的前項和為
，證明：
.
【答案】（1）
；（2）證明見解析.
【解析】試題分析：(1)由
時，利用
，結合等差數列的定義和通項公式即可得到數列
的通項公式；（2）由（1）得
，運用裂項相消法求和，化簡整理，然后利用放縮法可證明
.
試題解析：(1)當n=1時,a1=S1=3;
當n≥2時,an=Sn-Sn-1=n2+2n-
=2n+1.
當n=1時,也符合上式,故an=2n+1
.
(2)因為
=
=
,
故Tn=
=
【方法點晴】裂項相消法是最難把握的求和方法之一，其原因是有時很難找到裂項的方向，突破這一難點的方法是根據式子的結構特點，常見的裂項技巧：(1)
；（2） 
； （3）
；（4）
；此外，需注意裂項之后相消的過程中容易出現丟項或多項的問題，導致計算結果錯誤.
步步高達標卷系列答案科目：高中數學 來源： 題型：
【題目】已知公差不為0的等差數列{an}的前n項和為Sn，滿足S3＝a4＋4，且a2，a6，a18成等比數列．
(1)求數列{an}的通項公式；
(2)設bn＝
，求數列{bn}的前n項和Tn．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把函數 
的圖象上每個點的橫坐標擴大到原來的4倍，再向左平移 
，得到函數g（x）的圖象，則函數g（x）的一個單調遞減區間為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，已知點P（ 
，1），直線l的參數方程為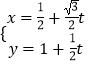 
（t為參數）若以O為極點，以Ox為極軸，選擇相同的單位長度建立極坐標系，則曲線C的極坐標方程為ρ= 
cos（θ- 
）
（Ⅰ）求直線l的普通方程和曲線C的直角坐標方程；
（Ⅱ）設直線l與曲線C相交于A，B兩點，求點P到A，B兩點的距離之積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=xe2x﹣lnx﹣ax．
（1）當a=0時，求函數f（x）在[ 
，1]上的最小值；
（2）若x＞0，不等式f（x）≥1恒成立，求a的取值范圍；
（3）若x＞0，不等式f（ 
）﹣1≥ e 
+ 
恒成立，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把函數 
的圖象上每個點的橫坐標擴大到原來的4倍，再向左平移 
，得到函數g（x）的圖象，則函數g（x）的一個單調遞減區間為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直三棱柱ABC﹣A1B1C1的底面為正三角形，E，F分別是A1C1 ， B1C1上的點，且滿足A1E=EC1 ， B1F=3FC1 ． 
（1）求證：平面AEF⊥平面BB1C1C；
（2）設直三棱柱ABC﹣A1B1C1的棱長均相等，求二面角C1﹣AE﹣B的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ex+ax，（a∈R），其圖象與x軸交于A（x1 ， 0），B（x2 ， 0）兩點，且x1＜x2
（1）求a的取值范圍；
（2）證明： 
；（f′（x）為f（x）的導函數）
（3）設點C在函數f（x）的圖象上，且△ABC為等邊三角形，記 
，求（t﹣1）（a+ 
）的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
