【答案】
分析:(1)先設出過P的切線方程,與拋物線方程聯立,因為切線與拋物線只可能有一個交點,所以∴△=0,就可求出兩條切線的斜率之積,再用導數求出曲線在A,B點的切線斜率,用A,B點的橫坐標表示,就可得到A,B點的橫坐標的關系式,因為M時A,B的中點,把M點坐標用A,B點坐標表示,代入前面求出的A,B橫坐標滿足的關系式,消去參數,就可得到M點的軌跡方程.
(2)利用導數,求出曲線在A,B點的切線斜率,把兩條切線方程都用以A,B點坐標為參數的方程表示,觀察兩個方程,形式相同,都滿足y=2tx+2,所以可得到直線AB的方程為y=2tx+2.
(3)用點到直線的距離公式求出三角形PAB的高,用弦長公式求出線段AB長,代入
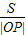
,化簡為直含t的式子,再用導數求出最小值.
解答:解:(1)設過P(t,0)與拋物線y=x
2+1的相切的直線的斜率是k,
則該切線的方程為:y=k(x-t)
由

,得,x
2-kx+(kt+1)=0
∵直線與拋物線相切,
∴方程x
2-kx+(kt+1)=0有一解,
∴△=k
2-4(kt+1)=k
2-4tk-4=0
則k
1,k
2都是方程k
2-4tk-4=0的解,故k
1k
2=-4
設A(x
1,y
1),B(x
2,y
2),M(x,y)
對函數y=x
2+1求導數,得y′=2x,
∴拋物線y=x
2+1在A(x
1,y
1)點處的切線斜率為2x
1,在B(x
2,y
2)點處的切線斜率為2x
2,
∴2x
1•2x
2=-4,即x
1x
2=-1
∵M為AB中點,∴x=
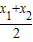
,y=
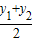
∵A,B點在拋物線y=x
2+1,∴y
1=x
12+1,y
2=x
22+1,
∴y
1+y
2=x
12+1+x
22+1=(x
1+x
2)
2-2x
1x
2+2
即2y=(2x)
2+2+2,2x
2-y+2=0
∴線段AB中點M的軌跡方程為2x
2-y+2=0
(2)由(1)知,直線PA的方程為y-y
1=2x
1(x-x
1),直線PB的方程為y-y
2=2x
2(x-x
2),
∵P(t,0)為兩條切線的交點,∴-y
1=2x
1(t-x
1),即-y
1=2x
1t-2x
12,
∵y
1=x
12+1,∴-y
1=2x
1t-2(y
1-1),y
1=2x
1t+2,同理,y
2=2x
2t+2,
∴直線AB的方程是y=2tx+2,則直線PQ過定點(0,2).
(3)P點到AB的距離d=
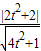
=
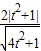
聯立直線AB與拋物線y=x
2+1,
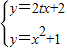
消去y,得,x
2-2tx-1=0
∴x
1+x
2=2t,x
1x
2=-1,∴|AB|=

|x
1-x
2|=
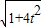

=
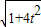
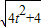
|OP|=|t|
∴
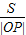
=
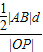
=

=

=2

(t≠0)
令
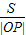
=m,則m=

對m求導,的m′=
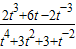
,令m′=0,得,t=-

,
∵當t<0時,m′<0.t>0時,m′>0,∴函數m=

在t=-
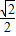
處有極小值,
又∵函數在整個定義域上只有一個極小值,
∴此時函數有最小值,也即

有最小值,最小值為
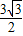
.
點評:本題主要考查直線與拋物線相切位置關系的判斷,導數與曲線的切線斜率之間的關系,以及應用導數求函數的最小值.

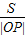 的最小值.
的最小值.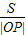 ,化簡為直含t的式子,再用導數求出最小值.
,化簡為直含t的式子,再用導數求出最小值. ,得,x2-kx+(kt+1)=0
,得,x2-kx+(kt+1)=0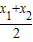 ,y=
,y=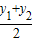
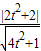 =
=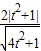
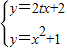 消去y,得,x2-2tx-1=0
消去y,得,x2-2tx-1=0 |x1-x2|=
|x1-x2|=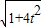
 =
=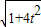
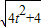
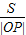 =
=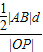 =
= =
= =2
=2 (t≠0)
(t≠0)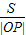 =m,則m=
=m,則m=
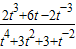 ,令m′=0,得,t=-
,令m′=0,得,t=- ,
, 在t=-
在t=-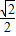 處有極小值,
處有極小值, 有最小值,最小值為
有最小值,最小值為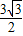 .
.

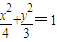 的中心,且焦點與該橢圓右焦點重合.
的中心,且焦點與該橢圓右焦點重合.