
【題目】已知橢圓![]() :
:![]() 的短軸長為
的短軸長為![]() ,離心率為
,離心率為![]() ,過右焦點
,過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() ,
,![]() .線段
.線段![]() 的垂直平分線交
的垂直平分線交![]() 軸于點
軸于點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)由題意可知:2b=2![]() ,
,![]() ,則a=2c,代入a2=b2+c2,求得a,即可求得橢圓C的標準方程;
,則a=2c,代入a2=b2+c2,求得a,即可求得橢圓C的標準方程;
(2)分類討論,設直線MN的方程為y=k(x﹣1)(k≠0),代入橢圓方程,求出線段MN的垂直平分線方程,令x=0,得![]() ,利用基本不等式,即可求
,利用基本不等式,即可求![]() 的取值范圍,再考慮斜率不存在的情況,取并集得到
的取值范圍,再考慮斜率不存在的情況,取并集得到![]() 的取值范圍.
的取值范圍.
(1)由題意可得:![]() ,
,![]() ,又
,又![]() ,
,
聯立解得![]() ,
,![]() ,
,![]() .
.
∴橢圓![]() 的方程為
的方程為![]() .
.
(2)當斜率存在時,設直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]() ,中點
,中點![]() ,
,
把![]() 代入橢圓方程,得到方程
代入橢圓方程,得到方程![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 的中垂線的方程為
的中垂線的方程為![]() ,令
,令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,則
,則![]() ;
;
當![]() 時,
時,![]() ,則
,則![]() ,
,
當斜率不存在時,顯然![]() ,
,
當![]() 時,
時,![]() 的中垂線為
的中垂線為![]() 軸.
軸.
綜上,![]() 的取值范圍是
的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】利用獨立性檢驗的方法調查大學生的性別與愛好某項運動是否有關,通過隨機詢問110名不同的大學生是否愛好某項運動,利用![]() 列聯表,由計算可得
列聯表,由計算可得![]()
P(K2>k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參照附表,得到的正確結論是( )
A.有99.5%以上的把握認為“愛好該項運動與性別無關”
B.有99.5%以上的把握認為“愛好該項運動與性別有關”
C.在犯錯誤的概率不超過0.05%的前提下,認為“愛好該項運動與性別有關”
D.在犯錯誤的概率不超過0.05%的前提下,認為“愛好該項運動與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 底面ABC,
底面ABC,![]() 是邊長為2的正三角形,
是邊長為2的正三角形,![]() ,E,F分別為BC,
,E,F分別為BC,![]() 的中點.
的中點.

![]() 1
1![]() 求證:平面
求證:平面![]() 平面
平面![]() ;
;
![]() 2
2![]() 求三棱錐
求三棱錐![]() 的體積;
的體積;
![]() 3
3![]() 在線段
在線段![]() 上是否存在一點M,使直線MF與平面
上是否存在一點M,使直線MF與平面![]() 沒有公共點?若存在,求
沒有公共點?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,四邊形ABCD是直角梯形,且AD∥BC,AD⊥CD,∠ABC=60°,BC=2AD=2,PC=3,△PAB是正三角形.
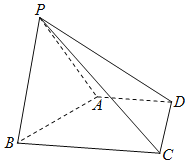
(1)求證:AB⊥PC;
(2)求二面角P﹣CD﹣B的平面角的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系 xOy中,O為坐標原點,已知點![]() ,P是動點,且三角形POQ的三邊所在直線的斜率滿足
,P是動點,且三角形POQ的三邊所在直線的斜率滿足![]() .
.
(1)求點P的軌跡C的方程;
(2)過F作傾斜角為60°的直線L,交曲線C于A,B兩點,求△AOB的面積;
(3)過點![]() 任作兩條互相垂直的直線
任作兩條互相垂直的直線![]() ,分別交軌跡 C 于點A,B和M,N,設線段AB,MN的中點分別為E,F.,求證:直線EF恒過一定點.
,分別交軌跡 C 于點A,B和M,N,設線段AB,MN的中點分別為E,F.,求證:直線EF恒過一定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除
給出求羨除體積的“術”是:“并三廣,以深乘之,又以袤乘之,六而一”,其中的“廣”指羨除的三條平行側棱的長,“深”指一條側棱到另兩條側棱所在平面的距離,“袤”指這兩條側棱所在平行線之間的距離,用現代語言描述:在羨除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,兩條平行線
,兩條平行線![]() 與
與![]() 間的距離為h,直線
間的距離為h,直線![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則該羨除的體積為
,則該羨除的體積為![]() 已知某羨除的三視圖如圖所示,則該羨除的體積為
已知某羨除的三視圖如圖所示,則該羨除的體積為![]()
![]()
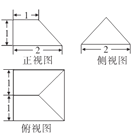
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com