
【題目】已知函數f(x)=xln x,g(x)=x3+ax2-x+2(a∈R).
(1)如果函數g(x)的單調遞減區間為![]() ,求函數g(x)的解析式;
,求函數g(x)的解析式;
(2)若不等式2f(x)≤![]() +2恒成立,求實數a的取值范圍.
+2恒成立,求實數a的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)求出![]() ,由函數g(x)的單調遞減區間為
,由函數g(x)的單調遞減區間為![]() 可得
可得![]() 是方程
是方程![]() 的兩根,根據韋達定理可求得
的兩根,根據韋達定理可求得![]() 的值,從而可得結果;(2)原不等式恒成立,等價于
的值,從而可得結果;(2)原不等式恒成立,等價于![]() 對
對![]() 恒成立,令
恒成立,令![]() ,利用導數研究函數
,利用導數研究函數![]() 的單調性,利用單調性求得h(x)最大值為-2,從而可得實數
的單調性,利用單調性求得h(x)最大值為-2,從而可得實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)g′(x)=3x2+2ax-1由題意3x2+2ax-1<0的解集是![]() ,
,
即3x2+2ax-1=0的兩根是-![]() 和1.
和1.
將x=1或-![]() 代入方程3x2+2ax-1=0得a=-1.
代入方程3x2+2ax-1=0得a=-1.
所以g(x)=x3-x2-x+2.
(2)2f(x)≤g′(x)+2對x∈(0,+∞)恒成立,
即:2xln x≤3x2+2ax+1對x∈(0,+∞)恒成立,
可得a≥ln x-![]() x-
x-![]() 對x∈(0,+∞)恒成立,
對x∈(0,+∞)恒成立,
設h(x)=ln x-![]() -
-![]() ,則h′(x)=
,則h′(x)=![]() -
-![]() +
+![]() =-
=-![]() ,
,
令h′(x)=0,得x=-![]() (舍)或x=1,
(舍)或x=1,
當0<x<1時,h′(x)>0;當x>1時,h′(x)<0,
所以當x=1時,h(x)取得最大值,最大值為-2,
所以a≥-2.
所以實數a的取值范圍是[-2,+∞).
【方法點晴】本題主要考查利用導數求函數的最值以及不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 即可)或
即可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.本題(2)是利用方法 ① 求得
恒成立;④ 討論參數.本題(2)是利用方法 ① 求得![]() 的取值范圍.
的取值范圍.


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了解某地區觀眾對某體育節目的收視情況,隨機抽取了100名觀眾進行調查,其中女性有55名,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
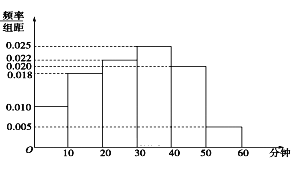
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據已知條件完成下面的22列聯表,并據此資料你是否認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為X.若每次抽取的結果是相互獨立的,求X的分布列,期望E(X)和方差D(X).
附:![]() .
.
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由![]() ,
,![]() ,
,![]() ,
,![]() 排列而成的
排列而成的![]() 項數列
項數列![]() 滿足:每項都大于它之前的所有項或者小于它之前的所有項.
滿足:每項都大于它之前的所有項或者小于它之前的所有項.
(![]() )滿足條件的數列中,寫出所有的單調數列.
)滿足條件的數列中,寫出所有的單調數列.
(![]() )當
)當![]() 時,寫出所有滿足條件的數列.
時,寫出所有滿足條件的數列.
(![]() )滿足條件的數列
)滿足條件的數列![]() 的個數是多少?并證明你的結論.
的個數是多少?并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】環境污染已經觸目驚心,環境質量已經成為“十三五”實現全面建成小康社會奮斗目標的短板和瓶頸。綿陽某化工廠每一天中污水污染指數![]() 與時刻
與時刻![]() (時)的函數關系為
(時)的函數關系為![]() 其中
其中![]() 為污水治理調節參數,且
為污水治理調節參數,且![]()
(1)若![]() ,求一天中哪個時刻污水污染指數最低;
,求一天中哪個時刻污水污染指數最低;
(2)規定每天中![]() 的最大值作為當天的污水污染指數,要使該廠每天的污水污染指數不超過
的最大值作為當天的污水污染指數,要使該廠每天的污水污染指數不超過![]() ,則調節參數
,則調節參數![]() 應控制在什么范圍內?
應控制在什么范圍內?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(ax+1)(x≥0,a>0), ![]() .
.
(1)討論函數y=f(x)-g(x)的單調性;
(2)若不等式f(x)≥g(x)+1在x∈[0,+∞)時恒成立,求實數a的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,角
,角![]() 的終邊經過點
的終邊經過點![]() .若
.若![]() 是
是![]() 的圖象上任意兩點,且當
的圖象上任意兩點,且當![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
(1)求 ![]() 或
或![]() 的值;
的值;
(2)求函數![]() 在
在![]() 上的單調遞減區間;
上的單調遞減區間;
(3)當![]() 時,不等式
時,不等式![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com