
【題目】下列命題: 1)y=|cos(2x+ ![]() )|最小正周期為π;
)|最小正周期為π;
2)函數y=tan ![]() 的圖象的對稱中心是(kπ,0),k∈Z;
的圖象的對稱中心是(kπ,0),k∈Z;
3)f(x)=tanx﹣sinx在(﹣ ![]() ,
, ![]() )上有3個零點;
)上有3個零點;
4)若 ![]() ∥
∥ ![]() ,
, ![]() ,則
,則 ![]()
其中錯誤的是
【答案】(1)(3)(4)
【解析】解:(1)函數y=cos(2x+ ![]() )最小正周期為π,則y=|cos(2x+
)最小正周期為π,則y=|cos(2x+ ![]() )|最小正周期為
)|最小正周期為 ![]() ;則(1)錯誤,(2)由
;則(1)錯誤,(2)由 ![]() =
= ![]() ,得x=kπ,即函數y=tan
,得x=kπ,即函數y=tan ![]() 的圖象的對稱中心是(kπ,0),k∈Z正確,則(2)正確;(3)由f(x)=tanx﹣sinx=0得,tanx=sinx,則sinx=0或cosx=1, 則在(﹣
的圖象的對稱中心是(kπ,0),k∈Z正確,則(2)正確;(3)由f(x)=tanx﹣sinx=0得,tanx=sinx,則sinx=0或cosx=1, 則在(﹣ ![]() ,
, ![]() )內,x=0,此時函數只有1個零點;則(3)錯誤,(4)若
)內,x=0,此時函數只有1個零點;則(3)錯誤,(4)若 ![]() ∥
∥ ![]() ,
, ![]() ,則
,則 ![]() 錯誤,當
錯誤,當 ![]() =
= ![]() 時,結論不成立,則(4)錯誤,
時,結論不成立,則(4)錯誤,
故錯誤的是(1)(3)(4),
所以答案是:(1)(3)(4)
【考點精析】認真審題,首先需要了解命題的真假判斷與應用(兩個命題互為逆否命題,它們有相同的真假性;兩個命題為互逆命題或互否命題,它們的真假性沒有關系).


科目:高中數學 來源: 題型:
【題目】已知二次函數 f (x) = x 2 + x,若不等式 f (-x) + f (x)≤2 | x | 的解集為C. (1)求集合C (2)若方程 f (a x)-a x + 1 = 5(a > 0,a≠1)在 C上有解,求實數 a 的取值范圍; (3)記 f (x) 在C 上的值域為 A,若 g(x) = x 3-3tx + ![]() ,x∈[0,1] 的值域為B,且 A B,求實數 t 的取值范圍.
,x∈[0,1] 的值域為B,且 A B,求實數 t 的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為菱形,∠ABC= ![]() ,PA⊥底面ABCD,PA=AB=2,M為PA的中點,N為BC的中點
,PA⊥底面ABCD,PA=AB=2,M為PA的中點,N為BC的中點 
(1)證明:直線MN∥平面PCD;
(2)求異面直線AB與MD所成角的余弦值;
(3)求點B到平面PCD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】漳州市博物館為了保護一件珍貴文物,需要在館內一種透明又密封的長方體玻璃保護罩內充入保護液體.該博物館需要支付的總費用由兩部分組成:①罩內該種液體的體積比保護罩的容積少0.5立方米,且每立方米液體費用500元;②需支付一定的保險費用,且支付的保險費用與保護罩容積成反比,當容積為2立方米時,支付的保險費用為4000元.
(Ⅰ)求該博物館支付總費用![]() 與保護罩容積
與保護罩容積![]() 之間的函數關系式;
之間的函數關系式;
(Ⅱ)求該博物館支付總費用的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“a≥3 ![]() ”是“直線l:2ax﹣y+2a2=0(a>0)與雙曲線C:
”是“直線l:2ax﹣y+2a2=0(a>0)與雙曲線C: ![]() ﹣
﹣ ![]() =1的右支無交點”的( )
=1的右支無交點”的( )
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f(x)是定義在(0,+∞)上的減函數,并且滿足f(xy)=f(x)+f(y), ![]() .
.
(1)求f(1)的值;
(2)如果f(x)+f(2﹣x)<2,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,點D在AB上. 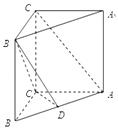
(1)若D是AB中點,求證:AC1∥平面B1CD;
(2)當 ![]() =
= ![]() 時,求二面角B﹣CD﹣B1的余弦值.
時,求二面角B﹣CD﹣B1的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com