
分析 由題意可得,當x∈(-∞,1]時,$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$>0,即當x∈(-∞,1]時,a•4x+3x+2x+1>0,分離參數a,利用函數的單調性求出g(x)=-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上的最大值得答案.
解答 解:由題意可知,當x∈(-∞,1]時,$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$>0,
即當x∈(-∞,1]時,a•4x+3x+2x+1>0,
∴a>-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上恒成立.
∵函數g(x)=-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上為增函數,
∴$g(x)_{max}=g(1)=-\frac{3}{2}$.
∴$a>-\frac{3}{2}$.
故a的取值范圍為($-\frac{3}{2},+∞$).
點評 本題考查函數的定義域及其求法,考查數學轉化思想方法,是中檔題.


 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $81\sqrt{3}$ | B. | $27\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 周期為4π的奇函數 | B. | 周期為4π的偶函數 | ||
| C. | 周期為π的奇函數 | D. | 周期為π的非奇非偶函數 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
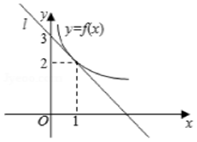 如圖所示,y=f(x)是可導函數,直線l:y=kx+3是曲線y=f(x)在x=1處的切線,若h(x)=xf(x),則h(x)在x=1處的切線方程為x-y+1=0.
如圖所示,y=f(x)是可導函數,直線l:y=kx+3是曲線y=f(x)在x=1處的切線,若h(x)=xf(x),則h(x)在x=1處的切線方程為x-y+1=0.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com