
【題目】定義函數![]() ,其中x為自變量,a為常數.
,其中x為自變量,a為常數.
(1)若當x∈[0,2]時,函數fa(x)的最小值為﹣1,求a的值;
(2)設全集U=R,集合A={x|f3(x)≥0},B={x|fa(x)+fa(2﹣x)=f2(2)},且(UA)∩B≠![]() 中,求a的取值范圍.
中,求a的取值范圍.
【答案】(1)3;(2)![]()
【解析】
(1)設t=2x,換元后,變為二次函數,確定新元取值范圍為![]() ,按對稱軸與區間
,按對稱軸與區間![]() 的關系求函數的最小值,從而可求得
的關系求函數的最小值,從而可求得![]() ;
;
(2)先求出集合UA,化簡方程由題意fa(x)+fa(2﹣x)=f2(2),題意說明![]() (a+1)(
(a+1)(![]() )+2a﹣6=0在(0,log23)內有解,換元設t
)+2a﹣6=0在(0,log23)內有解,換元設t![]() ,由指數函數及對勾函數性質得t∈[4,5),問題可以轉化為方程
,由指數函數及對勾函數性質得t∈[4,5),問題可以轉化為方程![]() 在t∈[4,5)上有解,只要求得
在t∈[4,5)上有解,只要求得![]() ,t∈[4,5)的值域即可,這又可由函數單調性得出.
,t∈[4,5)的值域即可,這又可由函數單調性得出.
(1)令t=2x,∵x∈[0,2],∴t∈[1,4],
設φ(t)=t2﹣(a+1)t+a,t∈[1,4],
1°當![]() ,即a≤1時,fmin(x)=φ(1)=0,與已知矛盾;
,即a≤1時,fmin(x)=φ(1)=0,與已知矛盾;
2°當![]() ,即
,即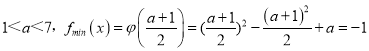 ,
,
解得a=3或a=﹣1,∵1<a<7,∴a=3;
3°當![]() ,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
,即a≥7,fmin(x)=φ(4)=16﹣4a﹣4+a=1,
解得![]() ,但與a≥7矛盾,故舍去,
,但與a≥7矛盾,故舍去,
綜上所述,a的值為3.
(2)UA={x|4x﹣42x+3<0}={x|0<x<log23},
B={x|4x﹣(a+1)2x+a+42﹣x﹣(a+1)22﹣x+a=6}![]() .
.
由已知(UA)∩B≠![]() 即
即![]() (a+1)(
(a+1)(![]() )+2a﹣6=0在(0,log23)內有解,
)+2a﹣6=0在(0,log23)內有解,
令t![]() ,則t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
,則t∈[4,5),方程(t2﹣8)﹣(a+1)t+2a﹣6在[4,5)上有解,
也等價于方程![]() 在t∈[4,5)上有解,
在t∈[4,5)上有解,
∵![]() 在t∈[4,5)上單調遞增,
在t∈[4,5)上單調遞增,
∴h(t)∈[﹣1,2),
故所求a的取值范圍是[﹣1,2).


科目:高中數學 來源: 題型:
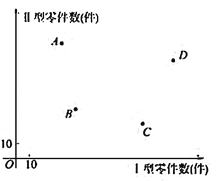
【題目】![]() 四名工人一天中生產零件的情況如圖所示,每個點的橫、縱坐標分別表示該工人一天中生產
四名工人一天中生產零件的情況如圖所示,每個點的橫、縱坐標分別表示該工人一天中生產
的Ⅰ型、Ⅱ型零件數,有下列說法:
四個工人中,![]() 的日生產零件總數最大
的日生產零件總數最大
②![]() 日生產零件總數之和小于
日生產零件總數之和小于![]() 日生產零件總數之和
日生產零件總數之和
③![]() 日生產Ⅰ型零件總數之和小于Ⅱ型零件總數之和
日生產Ⅰ型零件總數之和小于Ⅱ型零件總數之和
④![]() 日生產Ⅰ型零件總數之和小于Ⅱ型零件總數之和
日生產Ⅰ型零件總數之和小于Ⅱ型零件總數之和
則正確的說法有__________(寫出所有正確說法的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今年4月23日我市正式宣布實施“3+1+2”的高考新方案,“3”是指必考的語文、數學、外語三門學科,“1”是指在物理和歷史中必選一科,“2”是指在化學、生物、政治、地理四科中任選兩科.為了解我校高一學生在物理和歷史中的選科意愿情況,進行了一次模擬選科. 已知我校高一參與物理和歷史選科的有1800名學生,其中男生1000人,女生800人. 按分層抽樣的方法從中抽取了36個樣本,統計知其中有17個男生選物理,6個女生選歷史.
(I)根據所抽取的樣本數據,填寫答題卷中的列聯表. 并根據![]() 統計量判斷能否有
統計量判斷能否有![]() 的把握認為選擇物理還是歷史與性別有關?
的把握認為選擇物理還是歷史與性別有關?
(II)在樣本里選歷史的人中任選4人,記選出4人中男生有![]() 人,女生有
人,女生有![]() 人,求隨機變量
人,求隨機變量![]() 的分布列和數學期望.(
的分布列和數學期望.(![]() 的計算公式見下)
的計算公式見下)![]() ,臨界值表:
,臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)當![]() 時,求滿足方程
時,求滿足方程![]() 的
的![]() 的值;
的值;
(2)若函數![]() 是定義在R上的奇函數.
是定義在R上的奇函數.
①若存在![]() ,使得不等式
,使得不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
②已知函數![]() 滿足
滿足![]() ,若對任意
,若對任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最大值
的最大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,E,F,G分別是AB,CC1,AD的中點.
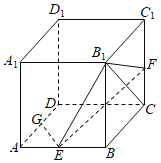
(1)求異面直線EG與B1C所成角的大小;
(2)棱CD上是否存在點T,使AT∥平面B1EF?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com