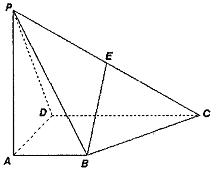
(本題滿分12分) 如圖,四棱錐P—ABCD的底面ABCD為一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中點。
(1)求證:BE//平面PAD;
(2)若BE⊥平面PCD,①求異面直線PD與BC所成角的余弦值;
②求二面角E—BD—C的余弦值。
設(shè)
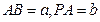
,建立如圖的空間坐標系,

,

,

,
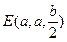
.……………………………………2分
(1)

,
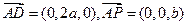
,
所以

,
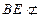
平面
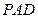
,
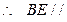
平面
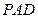
.

……………………………………4分
(2)

平面
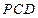
,
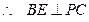
,即
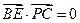

,
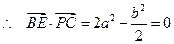
,即
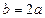
.………

…………6分
①
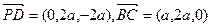
,

,
所以異面直線

與
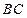
所成角的余弦值為
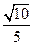
……………………………8分
②平面
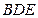
和平面
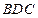
中,
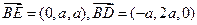
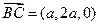
,
所以平面
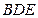
的一個法向量為
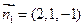
;……………………………………9分
平面

的一個法向量為
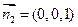
;……………………………………10分
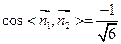
,所以二面角
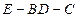
的余弦值為
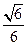
…………………12分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
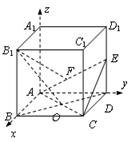
(滿分12分)正方體
ABCD-
A1B1C1D1 的棱長為 2,且
AC 與
BD 交于點
O,
E 為棱
DD1 中點,以
A 為原點,建立空間直角坐標系
A-
xyz,如圖所示.
(Ⅰ)求證:
B1O⊥平面
EAC;
(Ⅱ)若點
 F
F 在
EA 上且
B1F⊥
AE,試求點
F 的坐標;
(Ⅲ)求二面角
B1-
EA-
C 的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(.(本小題滿分12分)
如圖,四棱錐S-ABCD的底面是矩形,AB
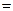 a
a,AD
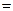
2,SA
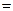
1,且SA⊥底面ABCD,若
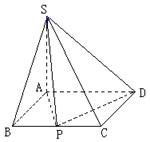
邊BC上存在異于B,C的一點P,使得
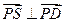
.
(1)求
a的最大值;
(2)當(dāng)
a取最大值時,求平面SCD的一

個單位法向量
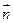
及點P到平面SCD的距離.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本題滿分10分)
如圖,在四邊形
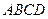
中,
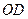
垂直平分
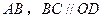
,且
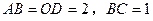
,現(xiàn)將四邊形
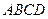
沿
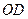
折成直二面角,求:
(1)求二面角
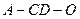
的正弦值;
(2)求三棱錐
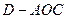
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本題滿分13分)
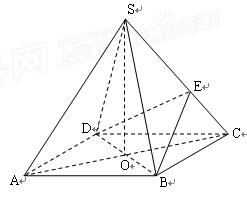
如圖,在四棱錐
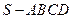
中,底面
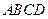
是正方形,其他四個側(cè)面都是等邊三角形,
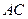
與
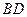
的交點為
O.
(Ⅰ)求證:
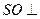
平面
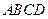
;
(Ⅱ)已知
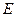
為側(cè)棱
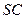
上一個動點. 試問對于
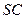
上任意一點
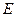
,平面
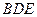
與平面
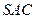
是否垂直?若垂直,請加以證明;若不垂直,請

說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
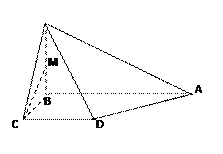
如圖,在四棱錐
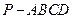
中,
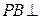
平面
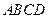
,

底面
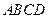
是一個直角梯形,
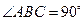
,
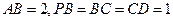
。
(1) 若
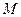
為
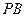
的中點,證明:直線
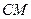
∥平面
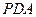
;
(2) 求二面角
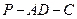
的余弦值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
如圖是某直三棱柱(側(cè)棱與底面垂直)被削去上底后的直觀圖與三視圖的側(cè)視圖、俯視圖,在直觀圖中,M是BD的中點,側(cè)視圖是直角梯形,俯視圖是等腰直角三角形,有關(guān)數(shù)據(jù)如圖所示.
(I)求出該幾何體的體積;
(II)求證:
EM∥平面
ABC;
(III)試問在棱
DC上是否存在點N,使NM⊥平面
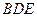
?若存在,確定點N的位置;

若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
異面直線a、b成60°,直線c⊥a,則直線b與c所成的角的范圍為 ( )
| A.[30°,90°] | B.[60°,90°] |
| C.[30°,60°] | D.[60°,120°] |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
在平面直角坐標系
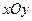
中,已知平面區(qū)域
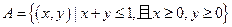
,則平面區(qū)域
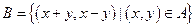
的面積為( )
| A.2 | B.1 | C.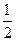 | D.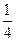 |
查看答案和解析>>


 F 在 EA 上且 B1F⊥AE,試求點 F 的坐標;
F 在 EA 上且 B1F⊥AE,試求點 F 的坐標;
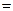 a,AD
a,AD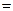 2,SA
2,SA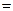 1,且SA⊥底面ABCD,若
1,且SA⊥底面ABCD,若
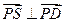 .
. 個單位法向量
個單位法向量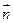
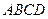 中,
中,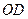 垂直平分
垂直平分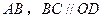 ,且
,且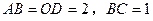 ,現(xiàn)將四邊形
,現(xiàn)將四邊形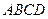 沿
沿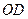 折成直二面角,求:
折成直二面角,求: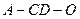 的正弦值;
的正弦值;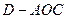 的體積.
的體積.
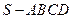 中,底面
中,底面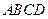 是正方形,其他四個側(cè)面都是等邊三角形,
是正方形,其他四個側(cè)面都是等邊三角形,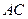 與
與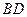 的交點為O.
的交點為O. 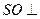 平面
平面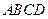 ;
;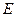 為側(cè)棱
為側(cè)棱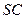 上一個動點. 試問對于
上一個動點. 試問對于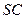 上任意一點
上任意一點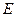 ,平面
,平面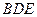 與平面
與平面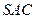 是否垂直?若垂直,請加以證明;若不垂直,請
是否垂直?若垂直,請加以證明;若不垂直,請 說明理由.
說明理由.
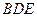 ?若存在,確定點N的位置;
?若存在,確定點N的位置; 若不存在,請說明理由.
若不存在,請說明理由.