久久精品国产99精品国产亚洲性色,日韩综合视频在线观看,日韩一区二区在线观看

【題目】下列說法正確的有_________.

①函數的一個對稱中心為；

②在中，是的中點，則；

③在中，是的充要條件；

④定義，已知，則的最大值為.

【答案】①②③④

【解析】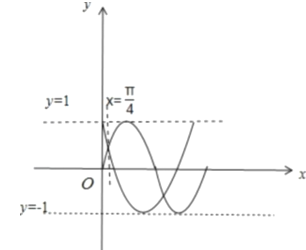

①對于函數，令，求得，故函數的圖象的一個對稱中心為，故①正確；②在中，是的中點，則，故②正確；③在中，，等價于，等價于，等價于，等價于，等價于，故③正確；④定義，已知，畫出和的圖象，如圖所示，則由圖可知，當時，取得最大值為，故④正確，故答案為①②③④.

【方法點睛】本題主要通過對多個命題真假的判斷，主要綜合考查向量的線性運算及三角函數的圖象與性質，屬于難題.這種題型綜合性較強，也是高考的命題熱點，同學們往往因為某一處知識點掌握不好而導致“全盤皆輸”，因此做這類題目更要細心、多讀題，盡量挖掘出題目中的隱含條件，另外，要注意從簡單的自己已經掌握的知識點入手，然后集中精力突破較難的命題.

練習冊系列答案

開心15天精彩寒假巧計劃江蘇鳳凰科學技術出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】2017年3月14日，“共享單車”終于來到蕪湖，共享單車又被親切稱作“小黃車”是全球第一個無樁共享單車平臺，開創了首個“單車共享”模式．相關部門準備對該項目進行考核，考核的硬性指標是：市民對該項目的滿意指數不低于，否則該項目需進行整改，該部門為了了解市民對該項目的滿意程度，隨機訪問了使用共享單車的名市民，并根據這名市民對該項目滿意程度的評分（滿分分），繪制了如下頻率分布直方圖：

（I）為了了解部分市民對“共享單車”評分較低的原因，該部門從評分低于分的市民中隨機抽取人進行座談，求這人評分恰好都在的概率；

（II）根據你所學的統計知識，判斷該項目能否通過考核，并說明理由．

（注：滿意指數=）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】過動點P作圓：（x﹣3）2+（y﹣4）2=1的切線PQ，其中Q為切點，若|PQ|=|PO|（O為坐標原點），則|PQ|的最小值是．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，四棱錐P﹣ABCD的底面ABCD是平行四邊形，側面PAD是邊長為2的正三角形，AB=BD= ，PB=
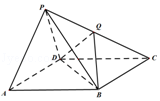
（Ⅰ）求證：平面PAD⊥平面ABCD；
（Ⅱ）設Q是棱PC上的點，當PA∥平面BDQ時，求二面角A﹣BD﹣Q的余弦值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知直線l1：x+2y+1=0，l2：-2x+y+2=0，它們相交于點A.

(1)判斷直線l1和l2是否垂直？請給出理由.

(2)求過點A且與直線l3：3x+y+4=0平行的直線方程.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】春節期間，受煙花爆竹集中燃放影響，我國多數城市空氣中PM2.5濃度快速上升，特別是在大氣擴散條件不利的情況下，空氣質量在短時間內會迅速惡化.2017年除夕18時和初一2時，國家環保部門對8個城市空氣中PM2.5濃度監測的數據如表（單位：微克/立方米）．

	除夕18時PM2.5濃度	初一2時PM2.5濃度
北京	75	647
天津	66	400
石家莊	89	375
廊坊	102	399
太原	46	115
上海	16	17
南京	35	44
杭州	131	39

（Ⅰ）求這8個城市除夕18時空氣中PM2.5濃度的平均值；
（Ⅱ）環保部門發現：除夕18時到初一2時空氣中PM2.5濃度上升不超過100的城市都是“禁止燃放煙花爆竹“的城市，濃度上升超過100的城市都未禁止燃放煙花爆竹．從以上8個城市中隨機選取3個城市組織專家進行調研，記選到“禁止燃放煙花爆竹”的城市個數為X，求隨機變量y的分布列和數學期望；
（Ⅲ）記2017年除夕18時和初一2時以上8個城市空氣中PM2.5濃度的方差分別為s12和s22 ，比較s12和s22的大小關系（只需寫出結果）．