Question

已知使函數f（x）=x³-ax²-1（0≤a≤M）存在整數零點的實數a恰有3個，則M的取值范圍是    ．

Answer 1

【答案】分析：由f（x）=0，解得．再利用a≥0即可得出x的取值范圍，從最小的整數x討論開始即可得出M的取值范圍．
解答：解：當x=0時，f（0）=-1≠0，即x=0不是函數f（x）的零點；
當x≠0時，由f（x）=0，解得．
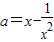
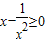
∵a≥0，∴，解得x≥1．
當x=1時，a=0，滿足題意；
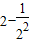
當x=2時，a==，滿足題意；
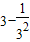
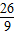
當x=3時，a==，滿足題意；
當x=4時，a==．
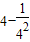
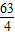
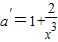
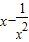
又∵＞0，∴當x≥1時，等單調遞增．
又∵函數f（x）存在整數零點的實數a恰有3個，∴M的取值范圍是．
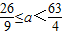
故答案為．
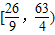
點評：利用函數零點的意義把問題正確等價轉化，熟練掌握分類討論的思想方法是解題的關鍵．