考點：橢圓的簡單性質(zhì)
專題：圓錐曲線的定義、性質(zhì)與方程
分析：由橢圓
+
=1方程可知，a，b，c 的值，由離心率e=
求出結(jié)果．
解答：
解：由橢圓
+
=1可知，a=2，b=
，c=1，∴離心率 e=
=
，
故選：C．
點評：本題考查橢圓的標(biāo)準(zhǔn)方程，以及橢圓的簡單性質(zhì)的應(yīng)用，求出a、c 的值是解題的關(guān)鍵．
練習(xí)冊系列答案
相關(guān)習(xí)題
科目：高中數(shù)學(xué)
來源：
題型：
設(shè)i是虛數(shù)單位，若（a+1）i=b+2i（a∈R，b∈R），則復(fù)數(shù)a+bi的模為
．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
在平面直角坐標(biāo)系xOy中，如果菱形OABC的邊長為2，點B在y軸上，則菱形內(nèi)（不含邊界）的整點（橫縱坐標(biāo)都是整數(shù)的點）個數(shù)的取值集合是（ ）
| A、{1，3} |
| B、{0，1，3} |
| C、{0，1，3，4} |
| D、{0，1，2，3，4} |
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知函數(shù)f（x）=ln（a+x）-ln（a-x）（a＞0）．
（Ⅰ）曲線y=f（x）在點（0，f（0））處的切線方程為y=2x，求a的值；
（Ⅱ）當(dāng)x≥0時，f（x）≥2x+
，試求a的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
在平面直角坐標(biāo)系中，橢圓
+=1（a＞b＞0）的焦距為2c（c＞0），以O(shè)為圓心，a為半徑作圓，過點（
，0）作圓的兩條切線互相垂直，則離心率e為（ ）
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
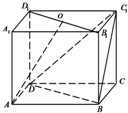
如圖．正方體ABCD-A
1B
1C
1D
1中，點O為B
1D
1的中點．求證：
（Ⅰ）AO∥面BC
1D；
（Ⅱ）AO⊥BD．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
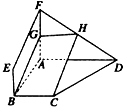
如圖，四邊形ABEF和ABCD都是直角梯形，∠BAD=∠FAB=90°，BE∥AF，BC∥AD，BC=
AD，BE=
AF，G、H分別為FA、FD的中點．
（1）在證明：四邊形BCHG是平行四邊形．
（2）C、D、F、E四點是否共面？若共面，請證明，若不共面，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知某幾何體的三視圖如圖所示，則該幾何體的體積為
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知l、m是不同的兩條直線，α、β是不重合的兩個平面，則下列命題中正確的是（ ）
| A、若l∥α，α⊥β，則l∥β |
| B、若l⊥α，α∥β，m?β，則l⊥m |
| C、若l⊥m，α∥β，m?β，則l⊥α |
| D、若l⊥α，α⊥β，則l∥β |
查看答案和解析>>
