
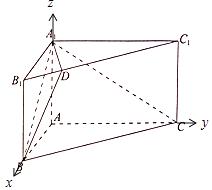
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=2 ![]() ,AA1=
,AA1= ![]() ,AB=2,點D在棱B1C1上,且B1C1=4B1D (Ⅰ)求證:BD⊥A1C
,AB=2,點D在棱B1C1上,且B1C1=4B1D (Ⅰ)求證:BD⊥A1C
(Ⅱ)求二面角B﹣A1D﹣C的大小.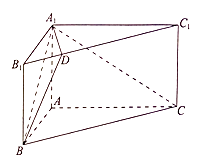
【答案】證明:(Ⅰ)分別以AB、AC、AA1所在直線為x、y、z軸建立空間直角坐標系, ∵AC=2 ![]() ,AA1=
,AA1= ![]() ,AB=2,點D在棱B1C1上,且B1C1=4B1D,
,AB=2,點D在棱B1C1上,且B1C1=4B1D,
∴B(2,0,0),C(0, ![]() ,0),A1(0,0,
,0),A1(0,0, ![]() ),D(
),D( ![]() ,
, ![]() ,
, ![]() ).
).
則 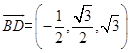 ,
, ![]() ,
,
∴ ![]() .
.
∴BD⊥A1C;
(Ⅱ)解:設平面BDA1的一個法向量為 ![]() ,
, ![]() ,
, 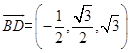 ,
,
∴ 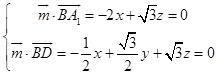 ,取z=2,則
,取z=2,則 ![]() ;
;
設平面A1DC的一個法向量為 ![]() ,
, 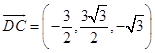 ,
, ![]() ,
,
∴ 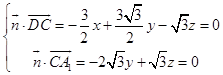 ,取y=1,得
,取y=1,得 ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
∴二面角B﹣A1D﹣C的大小為arccos ![]() .
.
【解析】(Ⅰ)分別以AB、AC、AA1所在直線為x、y、z軸建立空間直角坐標系,由已知得到所用點的坐標,求得 ![]() 的坐標,由兩向量的數量積為0說明BD⊥A1C;(Ⅱ)分別求出平面BDA1與平面A1DC的一個法向量,由兩法向量所成角的余弦值求得二面角B﹣A1D﹣C的大小.
的坐標,由兩向量的數量積為0說明BD⊥A1C;(Ⅱ)分別求出平面BDA1與平面A1DC的一個法向量,由兩法向量所成角的余弦值求得二面角B﹣A1D﹣C的大小.
【考點精析】通過靈活運用空間中直線與直線之間的位置關系,掌握相交直線:同一平面內,有且只有一個公共點;平行直線:同一平面內,沒有公共點;異面直線: 不同在任何一個平面內,沒有公共點即可以解答此題.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,{bn}是各項均為正數的等比數列,滿足a1=b1=1,b2﹣a3=2b3 , a3﹣2b2=﹣1
(1)求數列{an}和{bn}的通項公式
(2)設cn=an+bn , n∈N* , 求數列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了得到函數 ![]() 的圖象,只需把y=3sin2x上的所有的點( )
的圖象,只需把y=3sin2x上的所有的點( )
A.向左平行移動 ![]() 長度單位
長度單位
B.向右平行移動 ![]() 長度單位
長度單位
C.向右平行移動 ![]() 長度單位
長度單位
D.向左平行移動 ![]() 長度單位
長度單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面內到定點F(0,1)和定直線l:y=﹣1的距離之和等于4的動點的軌跡為曲線C,關于曲線C的幾何性質,給出下列四個結論: ①曲線C的方程為x2=4y;
②曲線C關于y軸對稱
③若點P(x,y)在曲線C上,則|y|≤2;
④若點P在曲線C上,則1≤|PF|≤4
其中,所有正確結論的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() =1(a>0,b>0)的離心率為
=1(a>0,b>0)的離心率為 ![]() ,過左焦點F1(﹣c,0)作圓x2+y2=a2的切線,切點為E,延長F1E交拋物線y2=4cx于P,Q兩點,則|PE|+|QE|的值為( )
,過左焦點F1(﹣c,0)作圓x2+y2=a2的切線,切點為E,延長F1E交拋物線y2=4cx于P,Q兩點,則|PE|+|QE|的值為( )
A.![]()
B.10a
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=log ![]() cos(
cos( ![]() ﹣2x)的遞增區間是 ( )
﹣2x)的遞增區間是 ( )
A.[﹣ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
B.[﹣ ![]() +kπ,kπ)(k∈Z)
+kπ,kπ)(k∈Z)
C.[ ![]() +kπ,
+kπ, ![]() +kπ](k∈Z)
+kπ](k∈Z)
D.[ ![]() +kπ,
+kπ, ![]() +kπ)(k∈Z)
+kπ)(k∈Z)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地一天從6時到14時的溫度變化曲線近似滿足函數y=Asin(ωx+φ)+b.
(1)求這一天的最大溫差;
(2)寫出這段曲線的函數解析式.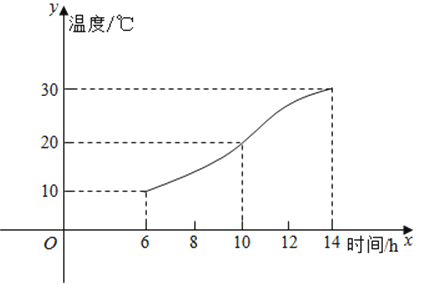
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com