
【題目】已知函數![]() ,
,![]() 是f(x)的導函數.
是f(x)的導函數.
(1)證明:當x>0時,f(x)>0;
(2)證明:![]() 在(
在(![]() )上有且只有3個零點.
)上有且只有3個零點.
【答案】(1)見解析(2)見解析
【解析】
(1)利用導數研究函數的單調性,利用單調性可證得不等式成立;
(2)轉化為證明![]() 在
在![]() 上有且只有3個零點,因為0是
上有且只有3個零點,因為0是![]() 的一個零點,再根據
的一個零點,再根據![]() 為奇函數,所以只需證明
為奇函數,所以只需證明![]() 在
在![]() 上有且只有一個零點,分兩種情況證明:①當
上有且只有一個零點,分兩種情況證明:①當![]() 時,利用導數證明
時,利用導數證明![]() ,此時
,此時![]() 無零點,②當
無零點,②當![]() 時,利用導數得到函數為單調函數,再根據零點存在性定理得
時,利用導數得到函數為單調函數,再根據零點存在性定理得![]() 有且只有一個零點.
有且只有一個零點.
(1)證明:![]()
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,
,
所以當![]() 時,
時,![]() .
.
(2)證明:![]() ,
,
令![]() ,得
,得![]() ,即
,即![]()
令![]() ,則
,則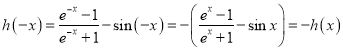 ,
,
![]() 是奇函數,且
是奇函數,且![]() ,即0是
,即0是![]() 的一個零點,
的一個零點,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
令![]() ,則
,則![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
由(1)知:當![]() 時,
時,![]() ,即
,即![]() ,
,
令![]() ,則
,則![]()
![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,
,![]() 單調遞減,
單調遞減,
又![]() ,
,
所以![]() 時,
時,![]() 恒成立,即
恒成立,即![]() 時,
時,![]() 恒成立,
恒成立,
所以當![]() 時,
時,![]() ,
,
所以當![]() 時,
時,![]() 恒成立,
恒成立,
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上為增函數,且
上為增函數,且 ,
,![]() ,
,
所以![]() 在
在![]() 上有且只有一個零點,設為
上有且只有一個零點,設為![]() ,所以
,所以![]() ,
,
因為![]() 是奇函數,
是奇函數,![]() ,
,
所以![]() 在
在![]() 上的零點為
上的零點為![]() ,
,
所以![]() 在
在![]() 上的零點為
上的零點為![]() ,
,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上有且只有3個零點.
上有且只有3個零點.
所以![]() 在
在![]() 上有且只有3個零點.
上有且只有3個零點.


科目:高中數學 來源: 題型:
【題目】已知在![]() 上任意一點
上任意一點![]() 處的切線
處的切線![]() 為
為![]() ,若過右焦點
,若過右焦點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() :
:![]() 于
于![]() 、
、![]() 兩點,在點
兩點,在點![]() 處切線相交于
處切線相交于![]() .
.
(1)求![]() 點的軌跡方程;
點的軌跡方程;
(2)若過點![]() 且與直線
且與直線![]() 垂直的直線(斜率存在且不為零)交橢圓
垂直的直線(斜率存在且不為零)交橢圓![]() 于
于![]() 兩點,證明:
兩點,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在銳角△ABC中,a=2![]() ,_______,求△ABC的周長l的范圍.
,_______,求△ABC的周長l的范圍.
在①![]() (﹣cos
(﹣cos![]() ,sin
,sin![]() ),
),![]() (cos
(cos![]() ,sin
,sin![]() ),且
),且![]()
![]() ,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x
,②cosA(2b﹣c)=acosC,③f(x)=cosxcos(x![]() )
)![]() ,f(A)
,f(A)![]()
注:這三個條件中任選一個,補充在上面問題中并對其進行求解.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,將其左、右焦點和短軸的兩個端點順次連接得到一個面積為
,將其左、右焦點和短軸的兩個端點順次連接得到一個面積為![]() 的正方形.
的正方形.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(均不在
兩點(均不在![]() 軸上),點
軸上),點![]() ,若直線
,若直線![]() 、
、![]() 、
、![]() 的斜率成等比數列,且
的斜率成等比數列,且![]() 的面積為
的面積為![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:3x+4y+m=0,圓C:x2+y2-4x+2=0,則圓C的半徑r=_____;若在圓C上存在兩點A,B,在直線l上存在一點P,使得∠APB=90°,則實數m的取值范圍是____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每到春夏交替時節,雌性楊樹會以滿天飛絮的方式來傳播下一代,漫天飛舞的楊絮易引發皮膚病、呼吸道疾病等,給人們造成困擾,為了解市民對治理楊絮方法的贊同情況,某課題小組隨機調査了部分市民(問卷調査表如下表所示),并根據調查結果繪制了尚不完整的統計圖表(如下圖)

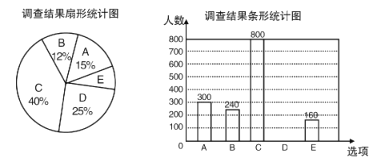
由兩個統計圖表可以求得,選擇D選項的人數和扇形統計圖中E的圓心角度數分別為( )
A.500,28.8°B.250,28.6°C.500,28.6°D.250,28.8°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將含有甲、乙、丙的6名醫護人員平均分成兩組到A、B兩家醫院參加“防疫救護”工作,則甲、乙至少有一人在A醫院且甲、丙不在同一家醫院參加“防疫救護”工作的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產某種電子產品,每件產品合格的概率均為![]() ,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗
,現工廠為提高產品聲譽,要求在交付用戶前每件產品都通過合格檢驗,已知該工廠的檢驗儀器一次最多可檢驗![]() 件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每
件該產品,且每件產品檢驗合格與否相互獨立.若每件產品均檢驗一次,所需檢驗費用較多,該工廠提出以下檢驗方案:將產品每![]() 個(
個(![]() )一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或
)一組進行分組檢驗,如果某一組產品檢驗合格,則說明該組內產品均合格,若檢驗不合格,則說明該組內有不合格產品,再對該組內每一件產品單獨進行檢驗,如此,每一組產品只需檢驗一次或![]() 次.設該工廠生產
次.設該工廠生產![]() 件該產品,記每件產品的平均檢驗次數為
件該產品,記每件產品的平均檢驗次數為![]() .
.
(1)![]() 的分布列及其期望;
的分布列及其期望;
(2)(i)試說明,當![]() 越大時,該方案越合理,即所需平均檢驗次數越少;
越大時,該方案越合理,即所需平均檢驗次數越少;
(ii)當![]() 時,求使該方案最合理時
時,求使該方案最合理時![]() 的值及
的值及![]() 件該產品的平均檢驗次數.
件該產品的平均檢驗次數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廠家在產品出廠前,需對產品做檢驗,廠家將一批產品發給商家時,商家按合同規定也需隨機抽取一定數量的產品做檢驗,以決定是否接收這批產品.
(1)若廠家庫房中(視為數量足夠多)的每件產品合格的概率為 ![]() 從中任意取出 3件進行檢驗,求至少有
從中任意取出 3件進行檢驗,求至少有![]() 件是合格品的概率;
件是合格品的概率;
(2)若廠家發給商家![]() 件產品,其中有
件產品,其中有![]() 不合格,按合同規定 商家從這
不合格,按合同規定 商家從這![]() 件產品中任取
件產品中任取![]() 件,都進行檢驗,只有
件,都進行檢驗,只有![]() 件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出的不合格產品的件數ξ的分布列,并求該商家拒收這批產品的概率.
件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出的不合格產品的件數ξ的分布列,并求該商家拒收這批產品的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com