
【題目】已知函數f(x)=ax3+cx+d(a≠0)是R上的奇函數,當x=1時,f(x)取得極值-2.
(1)求函數f(x)的解析式;
(2)求函數f(x)的單調區間和極大值;
(3)證明:對任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.
【答案】(1)f(x)=x3-3x;(2)f(x)的遞增區間是(-∞,-1)和(1,+∞);遞減區間為(-1,1).極大值為f(-1)=2;(3)證明見解析.
【解析】試題分析:(1)分析已知條件,函數為奇函數,即![]() ,可得
,可得![]() ,“當x=1時,f(x)取得極值-2”得
,“當x=1時,f(x)取得極值-2”得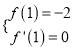 ,可解得
,可解得![]() ;(2)由
;(2)由![]() 確定增區間,由
確定增區間,由![]() 得減區間,從而確定極值點;(3)要證題設命題,只要求出
得減區間,從而確定極值點;(3)要證題設命題,只要求出![]() 在
在![]() 上的最大值和最小值,證明最大值-最小值≤4即可,為此可由第(2)小題的結論很快求得.
上的最大值和最小值,證明最大值-最小值≤4即可,為此可由第(2)小題的結論很快求得.
試題解析:(1)∵f(x)是R上的奇函數,
∴f(-x)=-f(x),
即-ax3-cx+d=-ax3-cx-d,∴d=-d,
∴d=0(或由f(0)=0得d=0).
∴f(x)=ax3+cx,f ′(x)=3ax2+c,
又當x=1時,f(x)取得極值-2,
∴ ,即
,即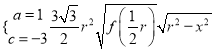 解得
解得![]()
∴f(x)=x3-3x.
(2)f ′(x)=3x2-3=3(x+1)(x-1),令f ′(x)=0,得x=±1,
當-1<x<1時,f ′(x)<0,函數f(x)單調遞減;
當x<-1或x>1時,f ′(x)>0,函數f(x)單調遞增;
∴函數f(x)的遞增區間是(-∞,-1)和(1,+∞);遞減區間為(-1,1).
因此,f(x)在x=-1處取得極大值,且極大值為f(-1)=2.
(3)由(2)知,函數f(x)在區間[-1,1]上單調遞減,且f(x)在區間[-1,1]上的最大值為M=f(-1)=2.最小值為m=f(1)=-2.∴對任意x1、x2∈(-1,1),
|f(x1)-f(x2)|<M-m=4成立.
即對任意x1、x2∈(-1,1),不等式|f(x1)-f(x2)|<4恒成立.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,得曲線
軸的正半軸為極軸建立極坐標系,得曲線![]() 的極坐標方程為
的極坐標方程為![]()
![]() .
.
(1)化曲線![]() 的參數方程為普通方程,化曲線
的參數方程為普通方程,化曲線![]() 的極坐標方程為直角坐標方程;
的極坐標方程為直角坐標方程;
(2)直線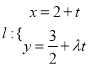 (
(![]() 為參數)過曲線
為參數)過曲線![]() 與
與![]() 軸負半軸的交點,求與直線
軸負半軸的交點,求與直線![]() 平行且與曲線
平行且與曲線![]() 相切的直線方程.
相切的直線方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.
(1)當a=1時,求函數f(x)的圖象在點(1,f(1))處的切線方程.
(2)是否存在實數a,對任意的x1,x2∈(0,+∞)且x1≠x2有![]() >a恒成立?若存在,求出a的取值范圍;若不存在,說明理由.
>a恒成立?若存在,求出a的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出x(單位:百萬元)與銷售額y(單位:百萬元)之間有如下的對應數據:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)畫出散點圖;
(2)求y關于x的線性回歸方程。
(3)如果廣告費支出為一千萬元,預測銷售額大約為多少百萬元?
參考公式
用最小二乘法求線性回歸方程系數公式: ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班主任對全班50名學生的學習積極性和對待班級工作的態度進行了調查,統計數據如下表所示:
積極參加班級工作 | 不太主動參加班級工作 | 合計 | |
學習積極性一般 | 6 | 19 | 25 |
合計 | 24 | 26 | 50 |
(1)如果隨機抽查這個班的一名學生,那么抽到積極參加班級工作的學生的概率是多少?抽到不太主動參加班級工作且學習積極性一般的學生的概率是多少?
(2)判斷是否有![]() 的把握認為學生的學習積極性與對待班級工作的態度有關系?
的把握認為學生的學習積極性與對待班級工作的態度有關系?
附:  , n=a+b+c+d.
, n=a+b+c+d.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間為了規定工時定額,需要確定加工零件所花費的時間,為此做了四次試驗,得到的數據如下表所示:
零件的個數x/個 | 2 | 3 | 4 | 5 |
加工的時間y/h | 2.5 | 3 | 4 | 4.5 |
(1)在給定的坐標系中畫出表中數據的散點圖;
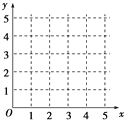
(2)求出y關于x的線性回歸方程![]() ,并在坐標系中畫出回歸直線;
,并在坐標系中畫出回歸直線;
(3)試預測加工10個零件需要多少時間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)判斷函數![]() 在
在![]() 和
和![]() 的單調性,并用定義證明
的單調性,并用定義證明![]() 在
在![]() 上的單調性;
上的單調性;
(2)若函數![]() 是定義域為
是定義域為![]() 的偶函數,且
的偶函數,且![]() 時,
時, ![]() ,
,
①當![]() 時,寫出
時,寫出![]() 的表達式;
的表達式;
②若函數![]() 有四個零點,寫出
有四個零點,寫出![]() 的取值范圍(不需要說明理由).
的取值范圍(不需要說明理由).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com