為配合國慶黃金周,促進旅游經濟的發展,某火車站在調查中發現:開始售票前,已有a人在排隊等候購票.開始售票后,排隊的人數平均每分鐘增b人.假設每個窗口的售票速度為c人/分鐘,且當開放兩個窗口時,25分鐘后恰好不會出現排隊現象(即排隊的人剛好購完);若同時開放三個窗口時,則15分鐘后恰好不會出現排隊現象.
(1)若要求售票10分鐘后不會出現排隊現象,則至少需要同時開幾個窗口?
(2)若a=60,在只開一個窗口的情況下,試求第n(n∈N*且n≤118)個購票者的等待時間tn關于n的函數,并求出第幾個購票者的等待時間最長?
(注:購票者的等待時間指從開即始排隊(售票開始前到達的人,從售票開始計時)到開始購票時止)
解:(1)設需同時開x個窗口,
則根據題意有,
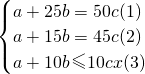
由(1)(2)得,c=2b,a=7b代入(3)得,75b+10b≤20bx,∴x≥4.25,
即至少同時開5個窗口才能滿足要求.
(2)由a=60得,b=0.8,c=1.6,設第n個人的等待時間為t
n,則由題意有,
當n≤60(n∈N
*)時,

;
當60<n≤118(n∈N
*)時,設第n個人是售票開始后第t分鐘來排隊的,
則n=60+0.8t,此時已有1.6t人購到票離開隊伍,即實際排隊的人數為n-1.6t,
∴
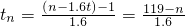
,
綜上,t
n關于n的函數為

,
∵當n≤60時,
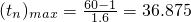
分鐘,
當60<n≤118時,
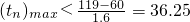
分鐘,
∴第60個購票者的等待時間最長.
分析:(1)由已知中每個窗口的售票速度為c人/分鐘,且當開放兩個窗口時,25分鐘后恰好不會出現排隊現象(即排隊的人剛好購完);若同時開放三個窗口時,則15分鐘后恰好不會出現排隊現象,我們可以構造關于a,b,c的方程,進而由售票10分鐘后不會出現排隊現象,構造一個關于x的不等式,即可得到答案.
(2)首先確定第n個人的等待時間的函數,分析其最值,即可得到結論.
點評:本題考查的知識點函數模型的選擇與應用,在利用函數模型,解答應用題時,解答的關鍵是根據已知條件求出函數的解析式,屬于中檔題.

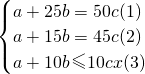
 ;
;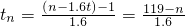 ,
, ,
,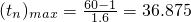 分鐘,
分鐘,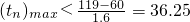 分鐘,
分鐘,

 黃岡冠軍課課練系列答案
黃岡冠軍課課練系列答案